Решите уравнение x3+7x2=4x+28.
x3+7x2=4x+28
x3+7x2-4x-28=0
x2(x+7)-4x-28=0
x2(x+7)-4(x+7)=0
Теперь вынесем за общую скобку (x+7):
(x+7)(x2-4)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два варианта:
1) x+7=0 => x1=-7
2) x2-4=0
x2-22=0
(x-2)(x+2)=0, следовательно:
x2=2
x3=-2
Ответ: x1=-7, x2=2, x3=-2
Поделитесь решением
Присоединяйтесь к нам...
Два бегуна одновременно стартовали в одном направлении из одного и того же места круговой трассы в беге на несколько кругов. Спустя один час, когда одному из них оставалось 1 км до окончания первого круга, ему сообщили, что второй бегун прошёл первый круг 20 минут назад. Найдите скорость первого бегуна, если известно, что она на 8 км/ч меньше скорости второго.
Решите неравенство 9x+8>8x-8.
1) (-∞;-16)
2) (-16;+∞)
3) (-∞;0)
4) (0;+∞)
Найдите наибольшее значение x, удовлетворяющее системе неравенств
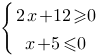
Решите неравенство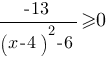 
Хозяин участка решил покрасить весь забор вокруг участка (только с внешней стороны) в зелёный цвет. Площадь забора равна 232 кв. м, а купить краску можно в одном из двух ближайших магазинов. Цены и характеристики краски даны в таблице.
| Номер магазина | Расход краски | Масса краски в одной банке | Стоимость одной банки краски | Стоимость доставки заказа |
| 1 | 0,6 кг/кв. м | 5 кг | 2400 руб. | 400 руб. |
| 2 | 0,4 кг/кв. м | 4 кг | 2300 руб. | 600 руб. |
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: