Сторона квадрата равна 40√2. Найдите радиус окружности, описанной около этого квадрата.
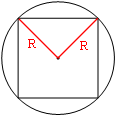Проведем отрезки из центра
квадрата к двум его углам, как на рисунке.
Заметим, что:
1) Эти отрезки и являются радиусами окружности.
2) Получившийся треугольник является
прямоугольным (по свойству квадрата).
Тогда мы можем применить
теорему Пифагора (пусть сторона квадрата - это "а"):
a2=R2+R2
a2=2R2
(40√2)2=2R2
По первому правилу действий со степенями:
402*(√2)2=2R2
402*2=2R2 |:2
402=R2
40=R
Ответ: 40
Поделитесь решением
Присоединяйтесь к нам...
Основания BC и AD трапеции ABCD равны соответственно 5 и 20, BD=10. Докажите, что треугольники CBD и BDA подобны.
Найдите площадь квадрата, описанного около окружности радиуса 32.
Периметр треугольника равен 50, одна из сторон равна 20,
а радиус вписанной в него окружности равен 4. Найдите площадь этого треугольника.
В треугольнике ABC биссектриса BE и медиана AD перпендикулярны и имеют одинаковую длину, равную 192. Найдите стороны треугольника ABC.
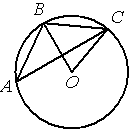Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: