Найдите площадь квадрата, описанного около окружности радиуса 32.
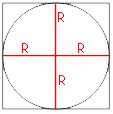Стороны
квадрата являются
касательными к окружности, следовательно, отрезок, проведенный от центра окружности к точке касания будет перпендикулярен стороне
квадрата и равен радиусу окружности (По
свойству касательной).
Получается, что сторона
квадрата равна диаметру окружности, или двум радиусам, т.е. 2*32=64
Площадь
квадрата равна произведению сторон:
S=64*64=4096
Ответ: 4096
Поделитесь решением
Присоединяйтесь к нам...
Укажите номера верных утверждений.
1) Существует ромб, который не является квадратом.
2) Если две стороны треугольника равны, то равны и противолежащие им углы.
3) Касательная к окружности параллельна радиусу, проведённому в точку касания.
Высота равностороннего треугольника равна 96√
Найдите величину угла DOK, если OK — биссектриса угла AOD, ∠DOB=64°. Ответ дайте в градусах.
В параллелограмме ABCD диагональ AC в 2 раза больше стороны AB и ∠ACD=104°. Найдите угол между диагоналями параллелограмма. Ответ дайте в градусах.
Точка D на стороне AB треугольника ABC выбрана так, что AD=AC. Известно, что ∠CAB=80° и ∠ACB=59°. Найдите угол DCB. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: