
Постройте график функции y=x2-4|x|+2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
В данной функции присутствуем
модуль, следовательно функцию надо разложить на две подфункции, в зависимости от значения
модуля:
 x2-4x+2x, при x≥0
x2-4x+2x, при x≥0
x2-4(-x)+2x, при x<0
 x2-2x, при x≥0
x2-2x, при x≥0
x2+6x, при x<0
Рассмотрим и построим график для каждой подфункции и объединим их.
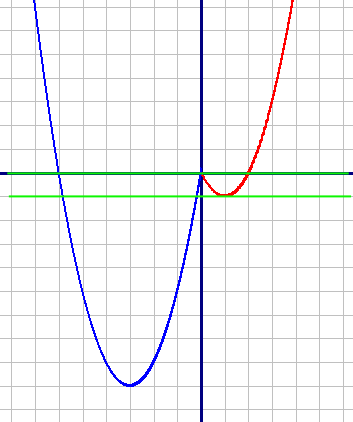 1) y1=x2-2x, при x≥0 (красный график)
1) y1=x2-2x, при x≥0 (красный график)
| X | 0 | 1 | 2 | 3 |
| Y | 0 | -1 | 0 | 3 |
| X | 0 | -1 | -2 | -3 | -4 | -5 |
| Y | 0 | -5 | -8 | -9 | -8 | -5 |
Поделитесь решением
Присоединяйтесь к нам...
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
КОЭФФИЦИЕНТЫ
А) k<0, b<0
Б) k<0, b>0
В) k>0, b<0
ГРАФИКИ
1)  2)
2)  3)
3) 
В таблице под каждой буквой укажите соответствующий номер.
Постройте график функции
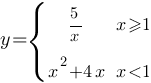 и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
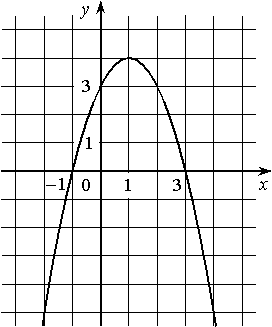 На рисунке изображён график квадратичной функции y=ƒ(x).
На рисунке изображён график квадратичной функции y=ƒ(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) ƒ(x)<0 при x<1
2) Наибольшее значение функции равно 3
3) ƒ(0)>ƒ(4)
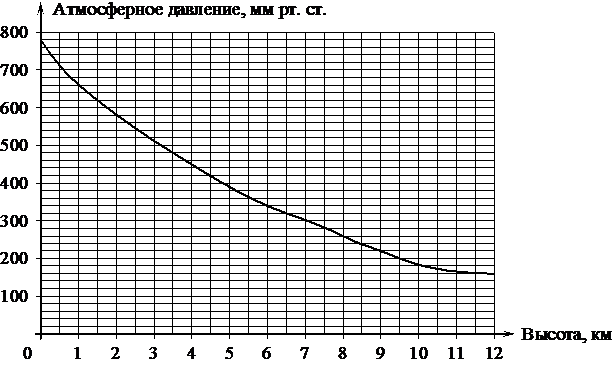 На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). Найдите, чему равно атмосферное давление на высоте 1 км. Ответ дайте в миллиметрах ртутного столба.
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты над уровнем моря (в километрах). Найдите, чему равно атмосферное давление на высоте 1 км. Ответ дайте в миллиметрах ртутного столба.
Постройте график функции y=x2-6|x|-2x и определите, при каких значениях c прямая y=c имеет с графиком ровно три общие точки.
Комментарии: