
Постройте график функции y=|x|x-|x|-3x и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Данная функция содержит
модуль, следовательно ее нужно разложить на две функции:
 x*x-x-3x, при x≥0
x*x-x-3x, при x≥0
(-x)x-(-x)-3x, при x<0
 x2-4x, при x≥0
x2-4x, при x≥0
-x2-2x, при x<0
 Обе подфункции - параболы. Построим их по точкам:
Обе подфункции - параболы. Построим их по точкам:
y1=x2-4x (красный график)
| X | 0 | 1 | 2 | 3 | 4 |
| Y | 0 | -3 | -4 | -3 | 0 |
| X | 0 | -1 | -2 | -3 |
| Y | 0 | 1 | 0 | -3 |
Поделитесь решением
Присоединяйтесь к нам...
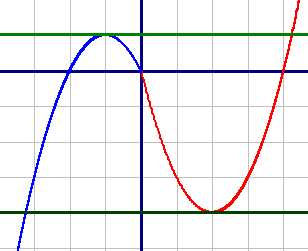
Постройте график функции
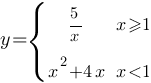 и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
и определите, при каких значениях c прямая y=c будет пересекать построенный график в трёх точках.
 На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 16 октября. Ответ дайте в градусах Цельсия.
На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наибольшую температуру воздуха 16 октября. Ответ дайте в градусах Цельсия.
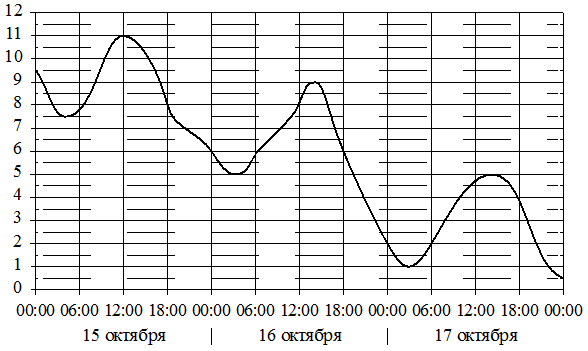
 На рисунке изображён график квадратичной функции y=f(x).
На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции являются верными? Запишите их номера.
1) f(-1)=f(5)
2) Функция убывает на промежутке [2; +∞)
3) f(x)>0 при x<-1 и при x>5
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между знаками коэффициентов k и b и графиками функций.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
А) k<0, b<0 Б) k<0, b>0 В) k>0, b<0 |
1)  |
2)  |
|
3)  |
4)  |
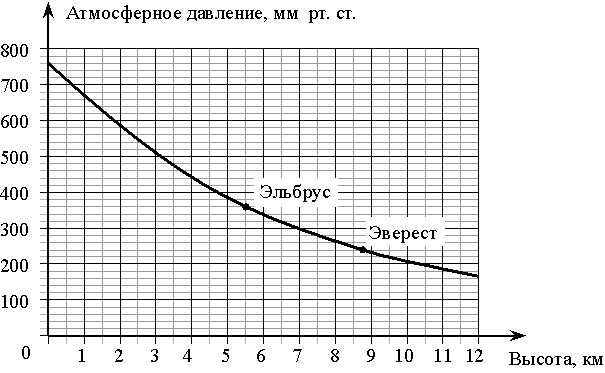 На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Эльбруса?
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Эльбруса?
Комментарии: