
Постройте график функции 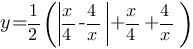 и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
и определите, при каких значениях m прямая y=m имеет с графиком ровно одну общую точку.
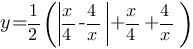
Область Допустимых Значений (ОДЗ).
x≠0 (так как делить на ноль нельзя).
Так как функция содержит
модуль, то ее надо разложить на две подфункции:
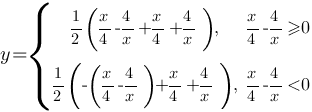
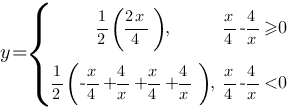
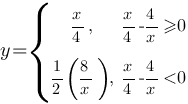
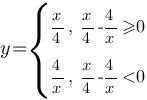
Теперь найдем для каких х 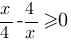 , а для каких х
, а для каких х 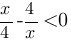
Найдем эти диапазоны:
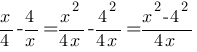
Дробь больше нуля в двух случаях:
1) Когда и числитель и знаменатель больше нуля.
2) Когда и числитель и знаменатель меньше нуля.
Эта же дробь будет меньше нуля на всех остальных диапазонах.
Рассмотрим первый вариант:
 x2-42≥0
x2-42≥0
4x>0
Чтобы решить систему неравенств нужно решить каждое неравенство по отдельности и пересечь полученные диапазоны.
 x2-42≥0
x2-42≥0
x>0
Диапазон второго неравенства (0;+∞), а диапазон для первого неравенства найдем, решив уравнение x2-42=0
 Воспользуемся формулой
разность квадратов:
Воспользуемся формулой
разность квадратов:
(x-4)(x+4)=0
x1=4
x2=-4
Коэффициент а=1, т.е. больше нуля, следовательно, ветви параболы направлены вверх. Значит диапазон для первого неравенства:
(-∞;-4]∪[4;+∞).
Пересекаем с диапазоном второго неравенства:
(-∞;-4]∪[4;+∞)∩(0;+∞)=[4;+∞)
Рассмотрим второй случай, когда и числитель и знаменатель меньше нуля.
 x2-42<0
x2-42<0
4x<0
 x2-42<0
x2-42<0
x<0
Эту систему решать не будем, а возьмем "обратные" диапазоны, т.е. для первого неравенства диапазон будет (-4;4), а для второго (-∞;0).
Пересекаем диапазоны:
(-4;4)∩(-∞;0)=(-4;0)
В итоге мы получили, что:
x/4-4/x≥0 на диапазонах (-4;0) и [4;+∞)
Следовательно:
x/4-4/x<0 на диапазонах (-∞;-4) и (0;4).
|
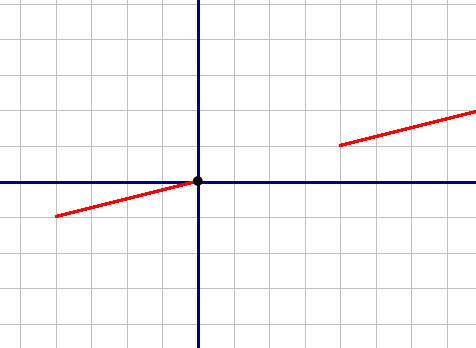
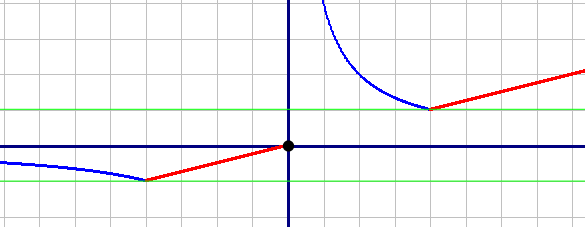
Построим график функции y1=x/4, при x∈(-4;0) и [4;+∞) - это прямая: Выкалываем точку x=0 (из ОДЗ).
| ||||||||||||
|
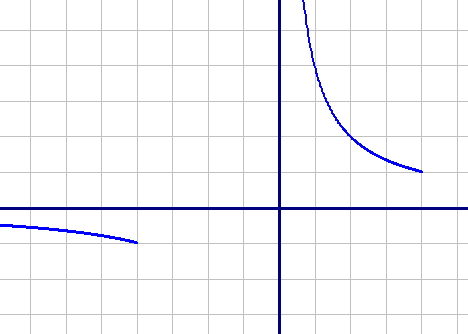
Вторая функция: y2=4/x, при x∈(-∞;-4) и (0;4) - это гипербола:
| ||||||||||||
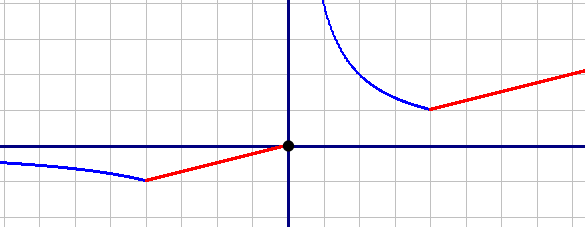
| Объединяем графики |
Поделитесь решением
Присоединяйтесь к нам...
На рисунках изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
ГРАФИКИ
А)  Б)
Б)  В)
В) 
КОЭФФИЦИЕНТЫ
1) k<0, b>0
2) k<0, b<0
3) k>0, b>0
В таблице под каждой буквой укажите соответствующий номер.
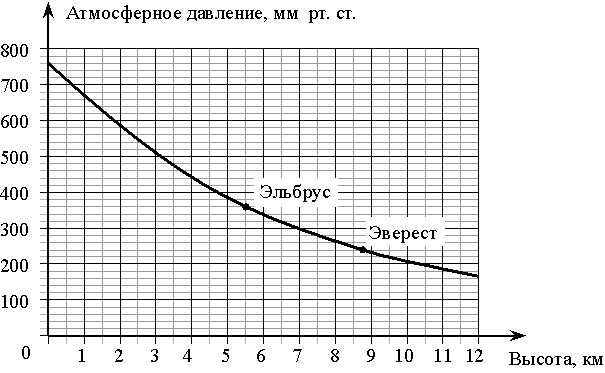 На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Эльбруса?
На графике изображена зависимость атмосферного давления (в миллиметрах ртутного столба) от высоты местности над уровнем моря (в километрах). На сколько миллиметров ртутного столба атмосферное давление на высоте Эвереста ниже атмосферного давления на высоте Эльбруса?
Установите соответствие между графиками функций и формулами, которые их задают.
| ФОРМУЛЫ | ГРАФИКИ | ||
|
1) y=x2+2 2) y=-2/x 3) y=2x 4) y=√ |
А)  |
Б)  |
В)  |
Постройте график функции
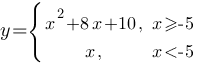
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
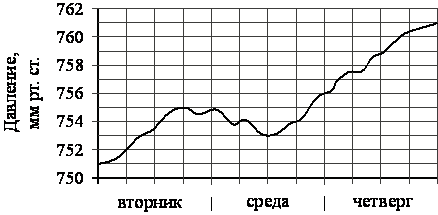 На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления в среду (мм рт. ст.).
На рисунке изображён график изменения атмосферного давления в городе Энске за три дня. По горизонтали указаны дни недели, по вертикали — значения атмосферного давления в миллиметрах ртутного столба. Укажите наименьшее значение атмосферного давления в среду (мм рт. ст.).
Комментарии: