Постройте график функции y=|x2-x-2|. Какое наибольшее число общих точек график данной функции может иметь с прямой, параллельной оси абсцисс?
Так как функция y=|x2-x-2| содержит
модуль, то данную функцию надо разложить на две функции, в зависимости от значения модуля.
y=x2-x-2, при x2-x-2≥0
y=-(x2-x-2), при x2-x-2<0
Вычислим при каких значениях х функция меняет свой знак, для этого решим неравенство:
x2-x-2≥0
Найдем
корни уравнения x2-x-2=0
D=(-1)2-4*1*(-2)=1+8=9
x1=(-(-1)+3)/(2*1)=4/2=2
x2=(-(-1)-3)/(2*1)=-2/2=-1
Решением данного неравенства будет диапазон (-∞; -1]∪[2; +∞), и меньше нуля в диапазоне (-1; 2).
Значит можем переписать систему:
y=x2-x-2, при x ∈ (-∞; -1]∪[2; +∞)
y=-(x2-x-2), при x ∈ (-1; 2)
Построим оба графика по точкам:
1) y=x2-x-2, при x ∈ (-∞; -1]∪[2; +∞) (красный график):
| X | -3 | -2 | -1 | 2 | 3 | 4 |
| Y | 10 | 4 | 0 | 0 | 4 | 10 |
| X | -1 | 0 | 1 | 2 |
| Y | 0 | 2 | 2 | 0 |
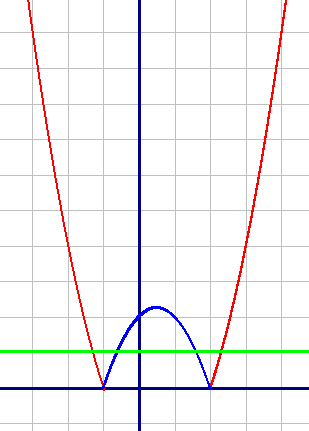Очевидно, что прямая, параллельная оси абсцисс будет иметь максимум 4 общие точки. Это видно на примере зеленой прямой.Поделитесь решением
Присоединяйтесь к нам...
Постройте график функции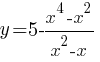 
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
На рисунке изображены графики функций вида y=kx+b. Установите соответствие между графиками функций и знаками коэффициентов k и b.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) k<0, b>0 2) k>0, b>0 3) k<0, b<0 4) k>0, b<0 |
А)  |
Б)  |
В)  |
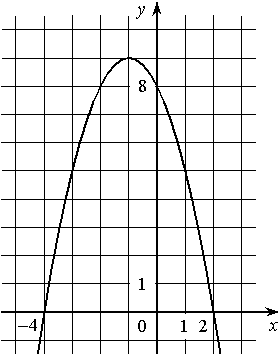На рисунке изображён график квадратичной функции y=f(x).
Какие из следующих утверждений о данной функции неверны? Запишите их номера.
1) Функция возрастает на промежутке (-∞;-1]
2) Наибольшее значение функции равно 8
3) f(-4)≠f(2)
Известно, что графики функций y=x2+p и y=-2x-2 имеют ровно одну общую точку. Определите координаты этой точки. Постройте графики заданных функций в одной системе координат.
На рисунке изображены графики функций вида y=ax2+bx+c. Установите соответствие между графиками функций и знаками коэффициентов a и c.
| КОЭФФИЦИЕНТЫ | ГРАФИКИ | ||
|
1) a<0, c>0 2) a<0, c<0 3) a>0, c<0 4) a>0, c>0 |
А)  |
Б)  |
В)  |
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2022-01-29 19:47:21) : дана функция у=х^-4х,х определи как должна быть расположена прямая параллельная оси абсцисс чтобы иметь с этим графиком ровно две общие точки
(2017-12-06 17:58:19) Администратор: Валентина, для знающего человека, конечно, проще так, как Вы сказали. Мое решение универсальное, чтобы показать, как вообще решаются подобные задачи с модулем.
(2017-12-03 16:10:06) Валентина: Зачем так сложно решать? Построили параболу и отразили ее симметрично относительно оси Ох.