
Решите систему уравнений 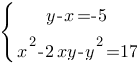
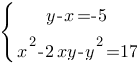
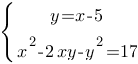
Подставим значение "y" во второе уравнение:
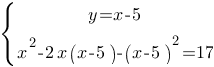
Раскроем обе скобки второго уравнения, для раскрытия второй скобки используем формулу
квадрат разности:

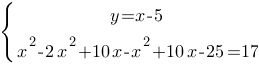
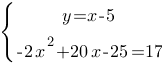
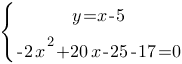
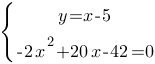
Разделим левую и правую части второго уравнения на (-2), чтобы упростить:
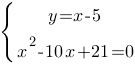
Решим второе уравнение через
дискриминант:
D=(-10)2-4*1*21=100-84=16
x1=(-(-10)+4)/(2*1)=(10+4)/2=7
x2=(-(-10)-4)/(2*1)=(10-4)/2=3
Теперь подставим в первое уравнение сначала x1, потом x2 и получим две пары ответов:
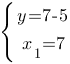
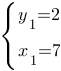
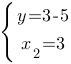
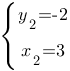
Ответ: (7;2) и (3;-2)
Поделитесь решением
Присоединяйтесь к нам...
Решите систему уравнений 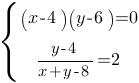
Решите уравнение (x-3)2(x-4)=2(x-3).
Решите уравнение 2x2+14x=0. Если уравнение имеет более одного корня, в ответ запишите меньший из корней.
Решите уравнение x3+4x2-x-4=0.
Принтер печатает одну страницу за 15 секунд. Сколько страниц можно напечатать на этом принтере за 2 минуты?
Комментарии: