Решите уравнение x(x2+2x+1)=2(x+1).
x(x2+2x+1)=2(x+1)
x(x2+2x+12)=2(x+1)
x(x+1)2=2(x+1) применена формула
квадрат суммы
x(x+1)2-2(x+1)=0
Выносим (x+1) за общие скобки:
(x+1)(x(x+1)-2)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два случая:
1) x+1=0
x1=-1
2) x(x+1)-2=0
x2+x-2=0
Решим это
квадратное уравнение при помощи
дискриминанта:
D=12-4*1*(-2)=1+8=9
X2=(-1+3)/(2*1)=2/2=1
X3=(-1-3)/(2*1)=-4/2=-2
Ответ: x1=-1, X2=1, X3=-2
Поделитесь решением
Присоединяйтесь к нам...
Решите уравнение x2-2x+√
Смешали некоторое количество 21%-го раствора некоторого вещества с таким же количеством 95%-го раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?
Решите неравенство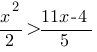 
Решите систему уравнений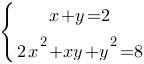 
Стоимость проезда в электричке составляет 249 рублей. Школьникам предоставляется скидка 50%. Сколько рублей будет стоить проезд для 2 взрослых и 3 школьников?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: