
Расстояние между пристанями А и В равно 140 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот прошёл 51 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч.
Скорость плота равна скорости реки.
Обозначим v - скорость лодки в неподвижной воде (т.е. собственная скорость).
v+3 - скорость лодки по течению.
v-3 - скорость лодки против течения.
Время лодки от пристани А до пристани В:
t1=140/(v+3)
Время лодки от пристани B до пристани A:
t2=140/(v-3)
Следовательно суммарное время лодки в пути:
t=t1+t2=140/(v+3)+140/(v-3)
За это же время +1 час плот проплыл 51 км со скоростью 3 км/ч:
t+1=51/3=17 часов
t=16 часов.
Возвращаемся к лодке, и получаем уравнение:
16=140/(v+3)+140/(v-3) |:4
4=35/(v+3)+35/(v-3) |:4
4=35(v-3)/((v+3)(v-3))+35(v+3)/((v-3)(v+3))
4=(35(v-3)+35(v+3))/((v-3)(v+3))
4
(v-3)(v+3)=35(v-3)+35(v+3)
4(v2-32)=35v-35*3+35v+35*3
4(v2-9)=35v+35v
4v2-36=70v
4v2-70v-36=0 |:2
2v2-35v-18=0
Решим это
квадратное уравнение:
D=(-35)2-4*2*(-18)=1225+144=1369
v1=(-(-35)+37)/(2*2)=72/4=18
v2=(-(-35)-37)/(2*2)=-2/4=-0,5
Отрицательной скорость быть не может, следовательно v=18 км/ч.
Ответ: 18
Поделитесь решением
Присоединяйтесь к нам...
Решите систему неравенств 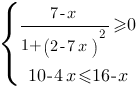
Решите уравнение 1-5x=-6x+8.
Решите неравенство (x-2)2<√
Первый велосипедист выехал из посёлка по шоссе со скоростью 18 км/ч. Через час после него со скоростью 16 км/ч из того же посёлка в том же направлении выехал второй велосипедист, а ещё через час — третий. Найдите скорость третьего велосипедиста, если сначала он догнал второго, а через 4 часа после этого догнал первого.
Рыболов проплыл на лодке от пристани некоторое расстояние вверх по течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся обратно через 5 часов от начала путешествия. На какое расстояние от пристани он отплыл, если скорость течения реки равна 2 км/ч, а собственная скорость лодки 6 км/ч?
Комментарии: