Найдите все значения k, при каждом из которых прямая y=kx имеет с графиком функции y=x2+0,25 ровно одну общую точку. Постройте этот график и все такие прямые.
Две функции имеют точку пересечения, это означает, что графики обеих функций имеют общую точку. Следовательно, надо составить систему и решить ее:
y=x2+0,25
y=kx
kx=x2+0,25
x2-kx+0,25=0
Найдем корни этого
уравнения:
D=(-k)2-4*1*0,25=k2-1
В условии сказано, что точка пересечения только одна, следовательно корень уравнения должен быть только один. Это условие выполняется, когда дискриминант равен нулю:
D=k2-1=0
k2=1
k1=1
k2=-1
Получаем функции:
y=x2+0,25
y=x
y=-x
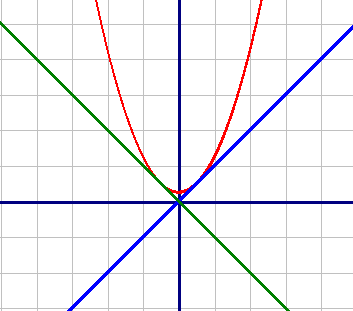построим графики по точкам:
y=x2+0,25 (красный)
| X | -2 | -1 | 0 | 1 | 2 |
| Y | 4,25 | 1,25 | 0,25 | 1,25 | 4,25 |
| X | -1 | 0 | 1 |
| Y | -1 | 0 | 1 |
| X | -1 | 0 | 1 |
| Y | 1 | 0 | -1 |
Поделитесь решением
Присоединяйтесь к нам...
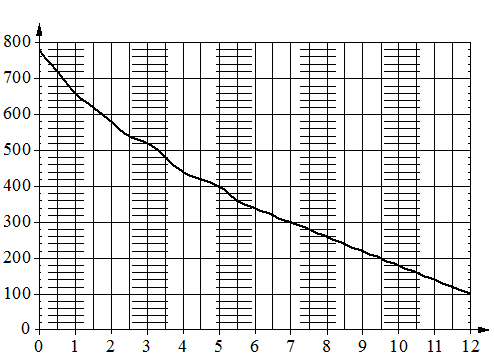На графике изображена зависимость атмосферного давления от высоты
над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной — давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление
на высоте 6 км над уровнем моря. Ответ дайте в миллиметрах ртутного столба.
Постройте график функции
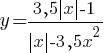
Определите, при каких значениях k прямая y=kx не имеет с графиком общих точек.
Установите соответствие между графиками функций и формулами, которые их задают.
ГРАФИКИ
A)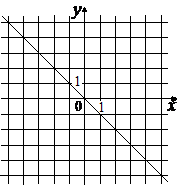 
Б) 
В) 
ФОРМУЛЫ
1) y=-x2
2) y=-x
3) y=-1/x
В таблице под каждой буквой укажите соответствующий номер.
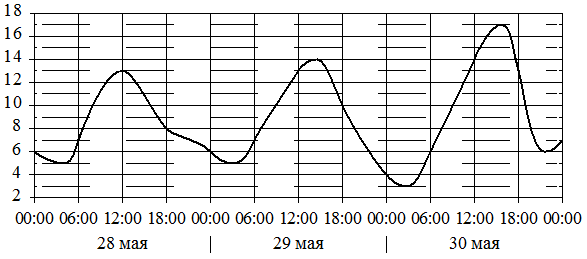На графике показано изменение температуры воздуха на протяжении трёх суток. По горизонтали указывается дата и время, по вертикали — значение температуры в градусах Цельсия. Определите по графику наименьшую температуру воздуха 30 мая. Ответ дайте в градусах Цельсия.
Постройте график функции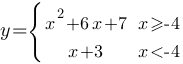 
и определите, при каких значениях m прямая y=m имеет с графиком ровно две общие точки.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-10-12 10:10:58) Администратор: Валерий, да, производные проходят только в 10-11 классах. Производная есть в каждой точке, но только в этих двух касательная будет иметь вид y=kx, во всех остальных точках будет вид y=kx+b (b не равно нулю), т.е. не будет проходить через начало координат.
(2015-10-12 10:05:20) Валерий.: Благодарю за ответ на моё обращение по этой задаче. Есть вопрос. Такой вариант решения предложен потому, что в 9 классе не изучают производную функции и уравнение касательной? Производная параболы существует в каждой точке её области определения, так я пониаю. Тогда в любой точке числовой прямой будет касательная и кроме прямой у=0,25 все остальные будут иметь вид у=kx.