
Какое наибольшее число последовательных натуральных чисел, начиная с 1, можно сложить, чтобы получившаяся сумма была меньше 561?
Иными словами, 1+2+3+4+...+n<561. Чему равен максимальный n?
Это
арифметическая прогрессия, разность прогрессии d=1, используем
формулу суммы:
Sn=(2*1+(n-1)*1)*n/2
Эта сумма должна быть меньше 561.
(2*1+(n-1)*1)*n/2<561
(2+n-1)n<1122
n2+n-1122<0
Решим это неравенство,
решив сначала уравнение n2+n-1122=0
D=12-4*1*(-1122)=1+4488=4489
n1=(-1+67)/(2*1)=66/2=33
n2=(-1-67)/(2*1)=-68/2=-34
Т.е. n∈(-34;33), заметьте крайние точки не включаются.
nmax=32
Ответ: 32
Поделитесь решением
Присоединяйтесь к нам...
Мотоцикл проехал x километров и израсходовал при этом 17 литров бензина. На сколько километров хватит 40 литров бензина при таких же условиях езды? Запишите соответствующее выражение.
Закон всемирного тяготения можно записать в виде 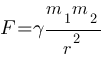 , где F — сила притяжения между телами (в ньютонах), m1 и m2 — массы тел (в килограммах), r — расстояние между центрами масс тел (в метрах), а γ — гравитационная постоянная, равная 6,67*10-11 Н*м2/кг2. Пользуясь этой формулой, найдите массу тела m1 (в килограммах), если F=4,002 Н, m2=4*109 кг, а r=2 м.
, где F — сила притяжения между телами (в ньютонах), m1 и m2 — массы тел (в килограммах), r — расстояние между центрами масс тел (в метрах), а γ — гравитационная постоянная, равная 6,67*10-11 Н*м2/кг2. Пользуясь этой формулой, найдите массу тела m1 (в килограммах), если F=4,002 Н, m2=4*109 кг, а r=2 м.
Найдите значение выражения 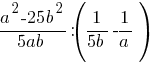 при
при 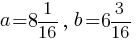 .
.
Найдите значение выражения (a+3)2-a(a-6) при a=-1/12.
Найдите значение выражения 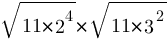
1) 1452
2) 132
3) 1584
4) 12√
Комментарии: