Решите уравнение x3+6x2=4x+24.
x3+6x2=4x+24
x3+6x2=4x+24
x2(x+6)=4(x+6)
x2(x+6)-4(x+6)=0
Выносим (x+6) за скобки:
(x+6)(x2-4)=0
(x+6)(x2-22)=0
Применим формулу разность квадратов:
(x+6)(x-2)(x+2)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим три варианта:
1) x+6=0 => x1=-6
2) x-2=0 => x2=2
3) x+2=0 => x3=-2
Ответ: x1=-6, x2=2, x3=-2
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения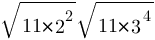 
1) 198
2) 18√
3) 3564
4) 2178
Сократите дробь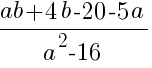 
Какое из данных ниже чисел является значением выражения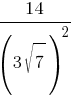 
1) 2/3
2) 2/9
3) 14/9
4) 14/3
Какое из данных ниже выражений при любых значениях n равно произведению 8*2n?
1) 16n
2) 23n
3) 2n+3
4) 8n+1
Найдите значение выражения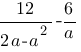 
при a=-23.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: