
Решите уравнение x(x2+2x+1)=6(x+1).
x(x2+2x+1)=6(x+1)
Заметим, что слагаемые в левой скобке представляют из себя квадрат суммы:
x(x2+2x+12)=6(x+1)
x(x+1)2=6(x+1)
x(x+1)2-6(x+1)=0
Вынесем (x+1) за общую скобку:
(x+1)(x(x+1)-6)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два случая:
1) x+1=0 => x1=-1
2) x(x+1)-6=0
x2+x-6=0
Решим это квадратное уравнение через дискриминант:
D=12-4*1*(-6)=1+24=25
x2=(-1+5)/(2*1)=4/2=2
x3=(-1-5)/(2*1)=-6/2=-3
Ответ: x1=-1, x2=2, x3=-3
Поделитесь решением
Присоединяйтесь к нам...
Укажите неравенство, которое не имеет решений.
1) x2+64<0
2) x2+64>0
3) x2-64>0
4) x2-64<0
Укажите неравенство, решение которого изображено на рисунке.

1) x2-7x<0
2) x2-49>0
3) x2-7x>0
4) x2-49<0
Известно, что число m отрицательное. На каком из рисунков точки с координатами 0, m, 2m, m2 расположены на координатной прямой в правильном порядке?
1) 
2) 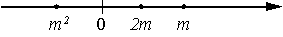
3) 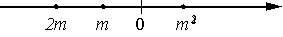
4) 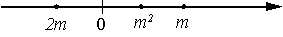
Решите уравнение x3+5x2=9x+45.
Решите уравнение x-6/x=-1.
Комментарии: