
Решите уравнение x3+5x2-x-5=0.
Первый вариант решения
x3+5x2-x-5=0
x2(x+5)-(x+5)=0
Вынесем (x+5) за общую скобку:
(x+5)(x2-1)=0
Произведение равно нулю, когда один из множителей равен нулю, поэтому рассмотрим два варианта:
1) x+5=0 => x1=-5
2) x2-1=0
x2-12=0
(x-1)(x+1)=0
x2=1
x3=-1
Второй вариант решения
Алгоритм такой:
1) Подобрать один из корней x1
2) Выполнить деление данного уравнения на (x-x1), получив квадратное уравнение.
3)
Решить полученное
квадратное уравнение с помощью
дискриминанта.
1) Попробуем подобрать первый корень, обычно это числа 1, -1, 2, -2, дальше искать не стоит, так как могут быть сложные вычисления.
Проверяем "1":
13+5*12-1-5=1+5-1-5=0, т.е. x1=1
2) Разделим x3+5x2-x-5 на (x-1):
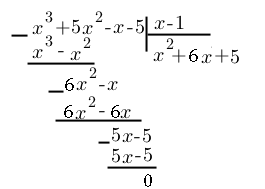
Таким образом получаем уравнение (x-1)(x2+6x+5)=0
3)
Найдем корни
квадратного уравнения x2+6x+5=0
D=62-4*1*5=36-20=16
x2=(-6+4)/(2*1)=-2/2=-1
x3=(-6-4)/(2*1)=-10/2=-5
Ответ: x1=1, x2=-1,
x3=-5
Поделитесь решением
Присоединяйтесь к нам...
Найдите значение выражения 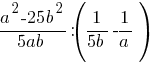 при
при 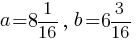 .
.
За 25 минут пешеход прошёл 2 километра. Сколько километров он пройдёт за t минут, если будет идти с той же скоростью? Запишите соответствующее выражение.
Найдите значение выражения 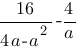 при a=-12.
при a=-12.
Решите уравнение (x2-25)2+(x2+3x-10)2=0.
Упростите выражение 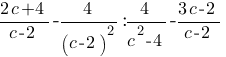
Комментарии:
(2017-05-02 22:55:47) Администратор: Мы не помогаем решить домашнее задание, цель сайта - подробно разобрать задачи, которые будут на экзаменах, чтобы учащиеся научились их решать самостоятельно. Если найдете похожую задачу на сайте fipi.ru, отправте заявку на добавление задачи, и мы ее обязательно добавим.
(2017-05-01 15:30:33) : xy+y^2/12x*6x/x+y