
Решите неравенство x2-25<0.
1) (-∞;+∞)
2) нет решений
3) (-5;5)
4) (-∞;-5)∪(5;+∞)
Для решения неравенства найдем корни
квадратного уравнения x2-25=0.
(x-5)(x+5)=0
Произведение равно нулю, когда один из множителей равен нулю, тогда:
1) x-5=0
x1=5
2) x+5=0
x2=-5
 График квадратичной функции - парабола.
График квадратичной функции - парабола.
Аргумент "а" равен 1, т.е. больше нуля, значит ветви параболы направлены вверх. Корни уравнения - точки пересечения графика функции оси Х.
Значение функции меньше нуля в диапазонах, где график располагается ниже оси Х, в данном случае (-5;5).
Ответ: 3)
Поделитесь решением
Присоединяйтесь к нам...
На каком рисунке изображено множество решений системы неравенств
 x+7≤0,5
x+7≤0,5
x+5≤0?
1) 
2) 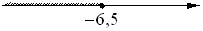
3) 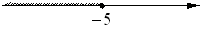
4) 
Решите неравенство 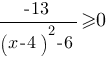
Расстояние между пристанями А и В равно 72 км. Из А в В по течению реки отправился плот, а через час вслед за ним отправилась моторная лодка, которая, прибыв в пункт В, тотчас повернула обратно и возвратилась в А. К этому времени плот проплыл 33 км. Найдите скорость лодки в неподвижной воде, если скорость течения реки равна 3 км/ч.
Два человека одновременно отправляются из одного и того же места по одной дороге на прогулку до опушки леса, находящейся в 4 км от места отправления. Один идёт со скоростью 2,7 км/ч, а другой — со скоростью 4,5 км/ч. Дойдя до опушки, второй с той же скоростью возвращается обратно. На каком расстоянии от точки отправления произойдёт их встреча?
Решите неравенство 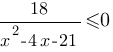
Комментарии: