Геометрическая прогрессия (bn) задана условиями: b1=-1, bn+1=2bn. Найдите b7.
Первый вариант решения, "в лоб"
b1=-1 (по условию)
b2=2b1=2*(-1)=-2
b3=2b2=2*(-2)=-4
b4=2b3=2*(-4)=-8
b5=2b4=2*(-8)=-16
b6=2b5=2*(-16)=-32
b7=2b6=2*(-32)=-64
Ответ: b7=-64
Поделитесь решением
Присоединяйтесь к нам...
Арифметическая прогрессия задана условиями a1=23, an+1=an-15. Найдите сумму первых 8 её членов.
В геометрической прогрессии сумма первого и второго членов равна 50, а сумма второго и третьего членов равна 200. Найдите первые три члена этой прогрессии.
Дана арифметическая прогрессия: 4; 7; 10; … . Найдите сумму первых шестидесяти пяти её членов.
Геометрическая прогрессия задана условиями b1=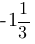
, bn+1=-3bn. Найдите b7.
Выписаны первые несколько членов арифметической прогрессии: -7; -4; -1; … Найдите сумму первых десяти её членов.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: