Дана геометрическая прогрессия (bn), знаменатель которой равен 2, b1=16. Найдите b4.
Каждый член
геометрической прогрессии можно выразить через первый член.
bn=b1qn-1
Следовательно, b4=b1q4-1=b1q3=16*23=16*8=128
Ответ: 128
Поделитесь решением
Присоединяйтесь к нам...
В геометрической прогрессии сумма первого и второго членов равна 144, а сумма второго и третьего членов равна 72. Найдите первые три члена этой прогрессии.
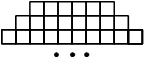Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 2 квадрата больше, чем в предыдущей. Сколько квадратов в 78-й строке?
В геометрической прогрессии сумма первого и второго членов равна 40, а сумма второго и третьего членов равна 160. Найдите первые три члена этой прогрессии.
Дана арифметическая прогрессия (an), разность которой равна -8,5, a1=-6,8. Найдите a11.
Последовательность задана условиями a1=3, an+1=an+4. Найдите a10.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-01-11 01:59:02) Администратор: Светлана, спасибо большое, что заметили ошибку. Все исправлено, еще раз спасибо.
(2015-01-10 20:51:17) Светлана: И если искать В4, то надо использовать формулу: В4= В1-q( в третьей степени). Тогда получается: 16*8=128. Ответ: В4=128
(2015-01-10 20:47:16) Светлана: Здесь Вас просят найти не сумму первых четырех членов прогрессии, а B4!!!