Геометрическая прогрессия (bn) задана условиями:
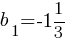, bn+1=-3bn.
Найдите b7.
В
геометрической прогрессии:
bn=b1qn-1
Найдем знаменатель прогрессии q:
bn=bn-1q или bn+1=bnq
q=bn+1/bn=-3 (по условию задачи).
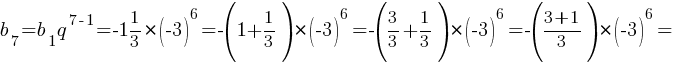
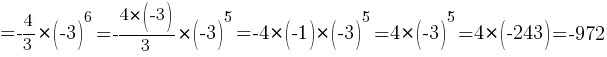
Jndtn^ -972
Поделитесь решением
Присоединяйтесь к нам...
Дана геометрическая прогрессия (bn), знаменатель которой равен 1/2, b1=2. Найдите сумму первых 4 её членов.
В первом ряду кинозала 24 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в восьмом ряду?
Геометрическая прогрессия задана условием bn=51,5(-2)n. Найдите b4.
Выписано несколько последовательных членов арифметической прогрессии: …; 1; x; -5; -8; … Найдите член прогрессии, обозначенный буквой x.
Геометрическая прогрессия задана условиями b1=-7, bn+1=3bn. Найдите сумму первых 5 её членов.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: