Дана арифметическая прогрессия (an), в которой a9=-15,7, a18=-22,9.
Найдите разность прогрессии.
Любой член
арифметической прогрессии можно записать через первый член прогрессии (a1) и разность прогрессии:
an=a1+(n-1)d
Тогда девятый член можно представить в следующем виде:
a9=a1+(9-1)d
-15,7=a1+8d
-15,7-8d=a1 (1) - это уравнение нам понадобится позже.
Восемнадцатый член можно представить так:
a18=a1+(18-1)d
-22,9=a1+17d
Подставляем значение a1 из уравнения (1):
-22,9=-15,7-8d+17d
-22,9+15,7=-8d+17d
-22,9+15,7=-8d+17d
-7,2=9d
d=-0,8
Ответ: -0,8
Поделитесь решением
Присоединяйтесь к нам...
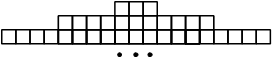Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 8 квадратов больше, чем в предыдущей. Сколько квадратов в 34-й строке?
Последовательность задана условиями a1=3, an+1=an-4. Найдите a10.
Дана арифметическая прогрессия (an), разность которой равна 6,8, a1=-3. Найдите a14.
Дана арифметическая прогрессия (an), разность которой равна 0,6 и a1=6,2. Найдите сумму первых шести её членов.
Выписано несколько последовательных членов арифметической прогрессии: -39; -30; -21; … Найдите первый положительный член этой прогрессии.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: