Последовательность задана формулой an=66/(n+1). Сколько членов этой последовательности больше 8?
Для решения этой задачи надо решить неравенство:
66/(n+1)>8
66>8(n+1)
66>8n+8
58>8n
29>4n
7,25>n
Так как в
арифметической прогрессии n - натуральное, то нас интересуют только целые положительные числа, т.е. от 1 до 7. Таким образом получается, что при n=1, 2, 3,..., 7, an будет больше 8.
Ответ: 7
Поделитесь решением
Присоединяйтесь к нам...
Дана арифметическая прогрессия (an), разность которой равна 6,8, a1=-3. Найдите a14.
В геометрической прогрессии сумма первого и второго членов равна 40, а сумма второго и третьего членов равна 160. Найдите первые три члена этой прогрессии.
Последовательность (bn) задана условиями:
b1=-6,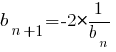 
.
Найдите b5.
Записаны первые три члена арифметической прогрессии: -9; -5; -1. Какое число стоит в этой арифметической прогрессии на 91-м месте?
Дана арифметическая прогрессия (an), разность которой равна -4,9, a1=-0,2. Найдите a7.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2015-04-23 15:50:59) Sonya: Спасибо огромнейшее! Много дней мучилась с этой темой и поняла только тогда, когда наткнулась на ваш сайт! Продолжайте работать в том же духе!