ОГЭ, Математика. Числовые последовательности: Задача №FED155 | Ответ-Готов

Юмор

Автор: Таська
Так выглядит современная программа обучения.
�...читать далее

ОГЭ, Математика.
Числовые последовательности: Задача №FED155

Задача №109 из 182
Условие задачи:

Последовательность задана условиями a₁=5, a_n+1=a_n+3. Найдите a₁₀.

Решение задачи:

Данная последовательность - арифметическая.
Разность d=a_n+1-a_n=3.
Любой член арифметической прогрессии можно выразить через a₁:
a_n=a₁+(n-1)d, тогда:
a₁₀=a₁+(10-1)d=5+9*3=5+27=32
Ответ: 32

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №2A803D

Геометрическая прогрессия (b_n) задана условиями:
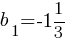, b_n+1=-3b_n.
Найдите b₇.

Задача №4B425F

В первом ряду кинозала 22 места, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в двенадцатом ряду?

Задача №00A508

Геометрическая прогрессия задана условием b_n=88*2ⁿ. Найдите сумму первых её 4 членов.

Задача №492D85

Геометрическая прогрессия задана условием b_n=62,5*2ⁿ. Найдите сумму первых её 4 членов.

Задача №19B940

Дана арифметическая прогрессия (a_n), в которой a₁₀=-10, a₁₆=-19.
Найдите разность прогрессии.

Комментарии:

Найти задачу

Подписаться на новости сайта

Хочу получать новые решения

email рассылки Ни какого спама

email рассылки

X Арифметическая прогрессия - числовая последовательность вида a₁, a₁+d, a₁+2d,..., a₁+(n-1)d,...то есть последовательность чисел (членов прогрессии), в которой каждое число, начиная со второго, получается из предыдущего добавлением к нему постоянного числа d (шага, или разности прогрессии):
a_n=a_n-1+d
Любой (n-й) член прогрессии может быть вычислен по формуле общего члена:
a_n=a₁+(n-1)d, где a₁ - первый член последовательности, d - ее разность.

X

Copyright otvet-gotov.ru 2014-2021. Все права защищены.