
Выписано несколько последовательных членов арифметической прогрессии: …; -9; x; -13; -15; … Найдите член прогрессии, обозначенный буквой x.
Любой член
арифметической прогрессии можно записать через предыдущий:
an=an-1+d
Пусть -9 - это n-ый член, тогда x - это (n+1)-ый член, -13 - это (n+2)-ой член, -15 - (n+3)-ий.
Значит:
x=-9+d
-13=x+d
-15=-13+d
Из последнего равенства d=-2
Подставляем d в первое равенство:
x=-9+d=-9+(-2)=-11
Ответ: x=-11
Поделитесь решением
Присоединяйтесь к нам...
Арифметическая прогрессия задана условием an=3,8-5,7n. Найдите a6.
Последовательность задана условиями a1=5, an+1=an+3. Найдите a10.
В геометрической прогрессии сумма первого и второго членов равна 120, а сумма второго и третьего членов равна 40. Найдите первые три члена этой прогрессии.
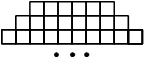 Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 2 квадрата больше, чем в предыдущей. Сколько квадратов в 78-й строке?
Фигура составляется из квадратов так, как показано на рисунке: в каждой следующей строке на 2 квадрата больше, чем в предыдущей. Сколько квадратов в 78-й строке?
Выписаны первые несколько членов арифметической прогрессии: -6; -3; 0; … Найдите сумму первых десяти её членов.
Комментарии:
(2023-05-04 15:05:08) ДОДИК 777: не понятно откуда d=-2
(2015-06-06 12:14:05) Администратор: Дима, в решении показано, как мы вычислили d.
(2015-05-26 18:29:34) дима: d=-2 как получается
(2015-05-24 14:35:03) Администратор: С какого момента непонятно?
(2015-05-24 12:46:25) : Ничего не понятно
(2015-05-24 12:46:22) : Ничего не понятно