
Хозяин договорился с рабочими, что они выкопают ему колодец на следующих условиях: за первый метр он заплатит им 3600 рублей, а за каждый следующий метр будет платить на 1400 рублей больше, чем за предыдущий. Сколько рублей хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 8 метров?
Условие задачи очень похоже на арифметическую прогрессию, где:
a1=3600
d=1400
А найти надо S8.
Воспользуемся формулой суммы арифметической прогрессии.
Для практики, найдем сумму сначала по первой формуле, а потом по второй:
1) Для первой формулы надо найти a8:
a8=a1+(n-1)d=3600+(8-1)1400=3600+7*1400=13400
S8 = n*(a1+a8)/2 = 8*(3600+13400)/2=8*17000/2 = 68000
2) Для второй формулы ничего дополнительно искать не надо:
S8 = n*(2a1+(n-1)d)/2 = 8*(2*3600+(8-1)1400)/2 = 8*(7200+7*1400)/2 = 8*(7200+9800)/2 = 8*17000/2 = 68000 руб.
Можно заменить, что вторая формула - это первая формула, только расписанная более подробно.
Ответ: 68000
Поделитесь решением
Присоединяйтесь к нам...
Сергей Петрович хочет купить в интернет-магазине микроволновую печь определённой модели. В таблице показано 6 предложений от разных интернет-магазинов.
| Номер магазина | Рейтинг магазина | Стоимость товара (руб.) | Стоимость доставки (руб.) |
| 1 | 3 | 12895 | 400 |
| 2 | 5 | 18490 | 0 |
| 3 | 5 | 13513 | 0 |
| 4 | 5 | 13745 | 390 |
| 5 | 4 | 13411 | 399 |
| 6 | 4 | 17489 | 0 |
Найдите значение выражения 38*10-1,3*102.
Список заданий викторины состоял из 33 вопросов. За каждый правильный ответ ученик получал 7 очков, за неправильный ответ с него списывали 12 очков, а при отсутствии ответа давали 0 очков. Сколько верных ответов дал ученик, набравший 70 очков, если известно, что по крайней мере один раз он ошибся?
Найдите значение выражения 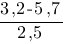
Найдите значение выражения 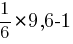
Комментарии: