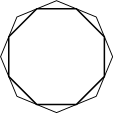
Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
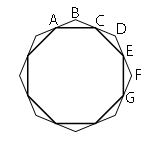Так как углы меньшего многоугольника располагаются на середине сторон, а сторон восемь, значит и углов будет восемь. Т.е. меньший многоугольник является восьмиугольником. Теперь докажем, что он правильный.
Рассмотрим треугольники ABC, CDE и EFG. AB=BC=CD=DE=EF=FG (по
определению правильного многоугольника).
/ABC=/CDE=/EFG (по
определению правильного многоугольника).
Следовательно, рассматриваемые треугольники равны (по
первому признаку равенства треугольников).
Это означает, что AC=CE=EG=GA.
Из равенства этих треугольников также следует, что все их острые углы тоже равны (/BAC=/BCA=/DCE=...и т.д.). Следовательно, /ACE=/CEG=...и так далее
В итоге, по
определению правильного многоугольника получается, меньший восьмиугольник - правильный.
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C прямой, AC=6, cosA=0,6. Найдите AB.
В треугольнике ABC AB=BC, а высота AH делит сторону BC на отрезки BH=3 и CH=1. Найдите cosB.
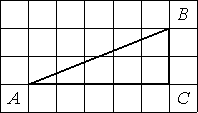Найдите тангенс угла А треугольника ABC, изображённого на рисунке.
Диагонали AC и BD трапеции ABCD с основаниями BC и AD пересекаются в точке O, BC=6, AD=13, AC=38. Найдите AO.
Сторона ромба равна 38, а острый угол равен 60°. Высота ромба, опущенная из вершины тупого угла, делит сторону на два отрезка. Каковы длины этих отрезков?
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: