
 Две касающиеся внешним образом в точке K окружности, радиусы которых равны 45 и 46, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
Две касающиеся внешним образом в точке K окружности, радиусы которых равны 45 и 46, вписаны в угол с вершиной A. Общая касательная к этим окружностям, проходящая через точку K, пересекает стороны угла в точках B и C. Найдите радиус окружности, описанной около треугольника ABC.
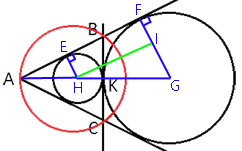 Проведем несколько отрезков:
Проведем несколько отрезков:
EH - радиус малой окружности. Он перпендикулярен AB (по
свойству касательной).
FG - радиус большой окружности. Он перпендикулярен AB (по
свойству касательной).
HG - отрезок, соединяющий центры окружностей и равный R+r, так как он проходит через точку К.
Рассмотрим треугольники AFG и AEH:
∠EAH - общий;
углы AEH и AFG - прямые.
Следовательно эти треугольники
подобны, тогда:
FG/EH=AG/AH
FG/EH=(AH+HG)/AH
46/45=(AH+R+r)/AH
46AH=45(AH+91)
46AH-45AH=4095
AH=4095
sin∠EAH=EH/AH=45/4095=1/91
AK=AH+r=4095+45=4140
AK перпендикулярен AB, т.к. это продолжение большого и малого радиусов, а AB -
касательная (
свойство касательной) и делит хорду AB пополам (по
свойству хорды).
Треугольник ABC -
равнобедренный, т.к. AK - и
медиана и
высота (
свойство равнобедренного треугольника).
Теперь уберем из рисунка все, что нас больше не интересует и резюмируем, что мы знаем:
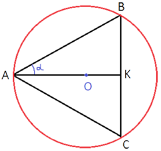 AK=4140
AK=4140
sinα=1/91
Так как AK -
биссектриса, то центр описанной окружности находится на AK.
Найдем AB.
По
теореме Пифагора:
AB2=AK2+BK2
AB2=AK2+(AB*sinα)2
AB2-AB2*sin2α=
41402
AB2(1-1/912)=41402
AB2(912-1)=912*41402
AB2=912*41402/(912-1)
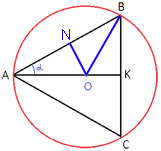 Рассмотрим треугольник AOB.
Рассмотрим треугольник AOB.
AO=OB, так как это радиусы окружности, следовательно данный треугольник
равнобедренный.
Проведем высоту ON, в
равнобедренном треугольнике она так же является и
медианой (по
свойству равнобедренного треугольника).
sinα=ON/AO=1/91 => ON=AO/91
По теореме
Пифагора:
AO2=ON2+AN2
AO2=AO2/912+(AB/2)2
AO2((912-1)/912)=912*41402/(912-1)
AO2=912*41402/(912-1)/((912-1)/912)=912*41402*912/(912-1)2
AO=912*4140/(912-1)
AO=8281*4140/8280=8281/2=4140,5
Ответ: Радиус описанной окружности равен 4140,5.
Поделитесь решением
Присоединяйтесь к нам...
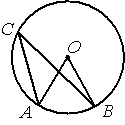 Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=84° (см. рисунок). Найдите величину угла ACB (в градусах).
 Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
Из точки А проведены две касательные к окружности с центром в точке О. Найдите радиус окружности, если угол между касательными равен 60°, а расстояние от точки А до точки О равно 6.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
 Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Дан правильный восьмиугольник. Докажите, что если последовательно соединить отрезками середины его сторон, то получится правильный восьмиугольник.
Какие из следующих утверждений верны?
1) Для точки, лежащей на окружности, расстояние до центра окружности равно радиусу.
2) Площадь трапеции равна произведению основания трапеции на высоту.
3) Треугольника со сторонами 1, 2, 4 не существует.
В ответ запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
Комментарии:
(2014-05-29 15:26:21) Танюшка: Большое спасибо! Очень мудреная задача!