
 В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
По второму свойству четырехугольника:
AB+CD=BC+AD=24
По
определению средней линии трапеции: m=(BC+AD)/2=24/2=12
Ответ: m=12
Поделитесь решением
Присоединяйтесь к нам...
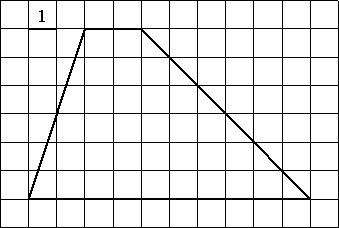 Найдите площадь трапеции, изображённой на рисунке.
Найдите площадь трапеции, изображённой на рисунке.
В прямоугольном треугольнике один из катетов равен 35, а угол, лежащий напротив него равен 45°. Найдите площадь треугольника.
Укажите номера верных утверждений.
1) В тупоугольном треугольнике все углы тупые.
2) В любом параллелограмме диагонали точкой пересечения делятся пополам.
3) Точка, лежащая на серединном перпендикуляре к отрезку, равноудалена от концов этого отрезка.
Стороны AC, AB, BC треугольника ABC равны 2√
 В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
 («простой»), должен быть выпуклым.
(«простой»), должен быть выпуклым.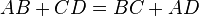
Комментарии: