В параллелограмме ABCD диагонали AC и BD пересекаются в точке K. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника AKD.
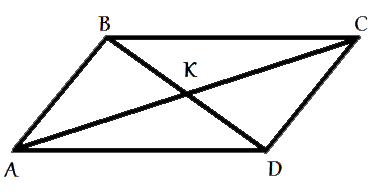Рассмотрим треугольники ABC и ACD.
Сторона AC - общая для этих треугольников.
AB=CD и BC=AD (по
свойству параллелограмма).
Следовательно, рассматриваемые треугольники равны (по
третьему признаку). А значит равны и их площади, и равны эти площади половине площади параллелограмма.
Рассмотрим треугольник ACD.
Как только что выяснили, площадь этого треугольника равна половине площади параллелограмма.
Отрезок DK - является
медианой (по третьему
свойству параллелограмма), и соответственно делит этот треугольник на два равновеликих треугольника, т.е. равных по площади (
свойство медианы).
Следовательно площадь AKD равна половине площади треугольника ACD.
SAKD=SACD/2=SABCD/4.
Поделитесь решением
Присоединяйтесь к нам...
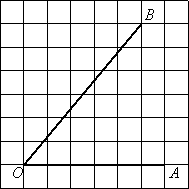Найдите тангенс угла AOB.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны AC втрое больше длины стороны AB. Найдите отношение площади треугольника BKP к площади треугольника AMK.
Найдите площадь треугольника, изображённого на рисунке.
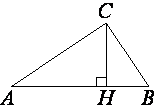В прямоугольном треугольнике ABC катет AC=65, а высота CH, опущенная на гипотенузу, равна 13√
Укажите номера верных утверждений.
1) Центры вписанной и описанной окружностей равнобедренного треугольника совпадают.
2) Существует параллелограмм, который не является прямоугольником.
3) Сумма углов тупоугольного треугольника равна 180°.
Хочу получать новые решения
Ни какого спама
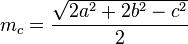, где mc — медиана к стороне c; a, b, c — стороны треугольника. В частности, сумма квадратов медиан произвольного треугольника в 4/3 раза меньше суммы квадратов его сторон: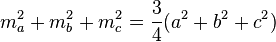 
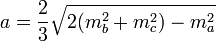, где ma, mb, mc медианы к соответствующим сторонам треугольника, a, b, c — стороны треугольника. 
Автор: Таська
Комментарии:
(2019-05-10 12:02:43) Администратор: Маша, DK - медиана по третьему свойству параллелограмма, которое гласит, что диагонали параллелограмма пересекаются и точкой пересечения делятся пополам. В решении есть ссылки на эти материалы, нажимайте на них.
(2019-05-10 09:50:42) Маша: Почему ДК является медианой и делит треугольник на 2 равновеликих треугольника,не очень понятно?
(2016-01-17 15:35:44) Маргарита: Спасибо огромное! Очень помогло)
(2015-05-24 18:28:57) Администратор: Антош, это свойство медианы.
(2015-05-24 18:12:51) Антош: А почему медиана делит на два равновеликих?
(2015-01-08 12:21:10) : cgfcb,j