В параллелограмме ABCD диагонали AC и BD пересекаются в точке O. Докажите, что площадь параллелограмма ABCD в четыре раза больше площади треугольника BOC.
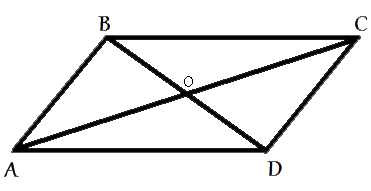Рассмотрим треугольники ABC и ACD.
Сторона AC - общая для этих треугольников, AB=CD и BC=AD (по
свойству параллелограмма), следовательно рассматриваемые треугольники равны (по
третьему признаку). А значит равны и их площади, и равны эти площади половине площади параллелограмма.
Рассмотрим треугольник ACD, как только что выяснили, площадь этого треугольника равна половине площади параллелограмма. Отрезок DO - является
медианой (по третьему
свойству параллелограмма), и соответственно делит этот треугольник на два равновеликих треугольника, т.е. равных по площади (
свойство медианы).
Следовательно площадь AOD равна половине площади треугольника ACD. SAOD=SACD/2=SABCD/4.
Поделитесь решением
Присоединяйтесь к нам...
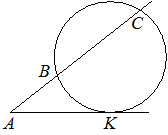Через точку A, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке K. Другая прямая пересекает окружность в точках B и C, причём AB=8, BC=24. Найдите AK.
Найдите площадь параллелограмма, изображённого на рисунке.
В треугольнике ABC проведена биссектриса AL, угол ALC равен 152°, угол ABC равен 137°. Найдите угол ACB. Ответ дайте в градусах.
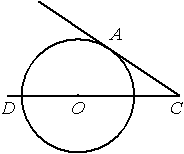Найдите угол АСО, если его сторона СА касается окружности, О — центр окружности, а дуга AD окружности, заключённая внутри этого угла, равна
110°.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
Хочу получать новые решения
Ни какого спама
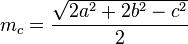, где mc — медиана к стороне c; a, b, c — стороны треугольника. В частности, сумма квадратов медиан произвольного треугольника в 4/3 раза меньше суммы квадратов его сторон: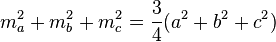 
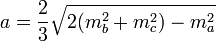, где ma, mb, mc медианы к соответствующим сторонам треугольника, a, b, c — стороны треугольника. 
Автор: Таська
Комментарии: