
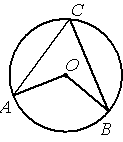
 Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
По условию /AOB=128°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 128°. /ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 128/2=64.
Ответ: /ACB=64°.
Поделитесь решением
Присоединяйтесь к нам...
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам.
 Площадь прямоугольного треугольника равна 968√
Площадь прямоугольного треугольника равна 968√
Какие из данных утверждений верны? Запишите их номера.
1) Если три угла одного треугольника соответственно равны трём углам другого треугольника, то такие треугольники подобны.
2) В любой четырёхугольник можно вписать окружность.
3) Центром описанной окружности треугольника является точка пересечения серединных перпендикуляров к его сторонам.
 Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=44, BC=24, CF:DF=3:1.
Прямая, параллельная основаниям трапеции ABCD, пересекает её боковые стороны AB и CD в точках E и F соответственно. Найдите длину отрезка EF, если AD=44, BC=24, CF:DF=3:1.
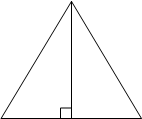 Высота равностороннего треугольника равна 96√
Высота равностороннего треугольника равна 96√
Комментарии: