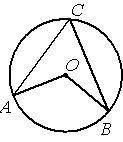
Точка О – центр окружности, /ACB=70° (см. рисунок). Найдите величину угла AOB (в градусах).
По условию /ACB=70°, этот угол является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 70°*2=140°.
/AOB является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /AOB=140°.
Ответ: /AOB=140°.
Поделитесь решением
Присоединяйтесь к нам...
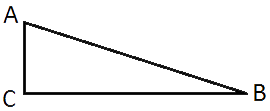Найдите площадь прямоугольного треугольника, если его катет и гипотенуза равны соответственно 28 и 100.
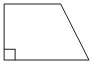Один из углов прямоугольной трапеции равен 121°. Найдите меньший угол этой трапеции. Ответ дайте в градусах.
Найдите угол ABC . Ответ дайте в градусах.
Имеются два сосуда, содержащие 12 кг и 8 кг раствора кислоты различной концентрации. Если их слить вместе, то получим раствор, содержащий 65% кислоты. Если же слить равные массы этих растворов, то полученный раствор будет содержать 60% кислоты. Сколько килограммов кислоты содержится во втором растворе?
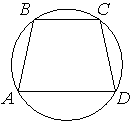Угол A трапеции ABCD с основаниями AD и BC, вписанной в окружность, равен 52°. Найдите угол B этой трапеции. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: