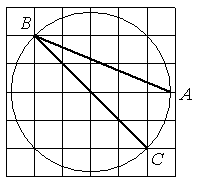
Найдите угол ABC. Ответ дайте в градусах.
Угол ABC (обозначим его α) является
вписанным в окружность, следовательно, он равен половине центрального угла, опирающегося на ту же дугу 2α (по
теореме).
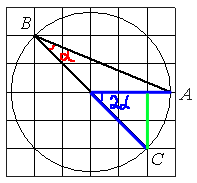Найдем
центральный угол через тангенс. Рассмотрим
центральный ("синий") угол и проведенный в нем катет ("зеленый").
tg(2α)=2/2=1
По
таблице угол 2α=45°
α=45°/2=22,5°
Ответ: 22,5
Поделитесь решением
Присоединяйтесь к нам...
В треугольнике ABC угол C равен 90°, sinB=3/7, AB=21. Найдите AC.
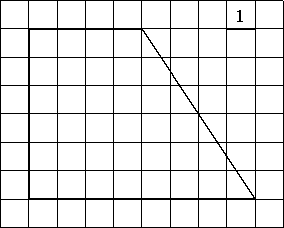Найдите площадь трапеции, изображённой на рисунке.
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 2 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1,5 м?
Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=15, AC=25.
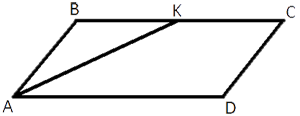Сторона BC параллелограмма ABCD вдвое больше стороны AB.
Точка K — середина стороны BC. Докажите, что AK — биссектриса
угла BAD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: