
 Углы при одном из оснований трапеции равны 50° и 40°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 13. Найдите основания трапеции.
Углы при одном из оснований трапеции равны 50° и 40°, а отрезки, соединяющие середины противоположных сторон трапеции, равны 15 и 13. Найдите основания трапеции.
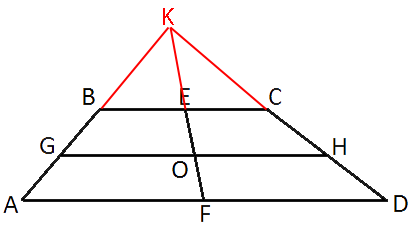 Продлим стороны AB и CD до пересечения в точке K.
Продлим стороны AB и CD до пересечения в точке K.
Рассмотрим треугольник AKD.
По
теореме о сумме углов треугольника:
∠AKD+∠KDA+∠DAK=180°
∠AKD+50°+40°=180°
∠AKD=90°
Следовательно треугольник AKD -
прямоугольный с гипотенузой AD.
KF -
медиана (по условию задачи).
Мысленно опишем вокруг этого треугольника окружность. Так как треугольник
прямоугольный, то центр окружности располагается на середине гипотенузы AD (по
теореме об описанной окружности).
Следовательно AF=FD=R - радиус окружности,
медиана KF тоже равна радиусу и, следовательно, равна AD/2.
Рассмотрим треугольник GKH.
Для этого треугольника KO -
медиана и равна половине гипотенузы GH (как и у предыдущего треугольника).
KO=OH=GH/2
В треугольнике BKC - аналогичная ситуация: KE=EC=BC/2
Вернемся к треугольнику GKH:
KO=OH=GH/2=15/2=7,5
7,5=OH=KE+EO=EC+EF/2
EC=7,5-EF/2=7,5-13/2=7,5-6,5=1
BC=2*EC=2*1=2
Рассмотрим трапецию ABCD.
GH -
средняя линия, следовательно GH=(BC+AD)/2
2GH=BC+AD
AD=2GH-BC=2*15-2=30-2=28
Ответ: AD=28, BC=2
Поделитесь решением
Присоединяйтесь к нам...
 Катет и гипотенуза прямоугольного треугольника равны 15 и 39. Найдите высоту, проведенную к гипотенузе.
Катет и гипотенуза прямоугольного треугольника равны 15 и 39. Найдите высоту, проведенную к гипотенузе.
 В треугольнике ABC угол C прямой, AC=8, cosA=0,4. Найдите AB.
В треугольнике ABC угол C прямой, AC=8, cosA=0,4. Найдите AB.
 В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
 Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
Найдите угол ABC равнобедренной трапеции ABCD, если диагональ AC образует с основанием AD и боковой стороной CD углы, равные 30° и 80° соответственно.
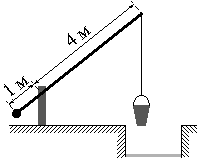 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Комментарии: