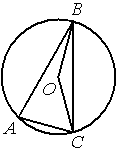
Точка О – центр окружности, /BAC=75° (см. рисунок). Найдите величину угла BOC (в градусах).
По условию /BAC=75°, этот угол является
вписанным углом и равен половине градусной меры дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 75°*2=150°.
/BOC является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /BOC=150°.
Ответ: /BOC=150°.
Поделитесь решением
Присоединяйтесь к нам...
На клетчатой бумаге с размером клетки 1x1 изображён параллелограмм. Найдите его площадь.
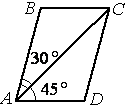Диагональ AC параллелограмма ABCD образует с его сторонами углы, равные 30° и 45°. Найдите больший угол параллелограмма.
Какие из данных утверждений верны? Запишите их номера.
1) Площадь квадрата равна произведению его диагоналей.
2) Если две различные прямые на плоскости перпендикулярны третьей прямой, то эти две прямые параллельны.
3) Вокруг любого параллелограмма можно описать окружность.
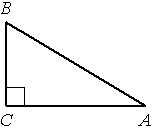В треугольнике ABC угол C прямой, BC=3, cosB=0,6. Найдите AB.
Высота AH ромба ABCD делит сторону CD на отрезки DH=24 и CH=2. Найдите высоту ромба.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: