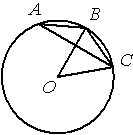
Точка О – центр окружности, /BAC=10° (см. рисунок). Найдите величину угла BOC (в градусах).
По условию /BAC=10°, этот угол является
вписанным углом и равен половине градусной меры дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 10°*2=20°.
/BOC является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /BOC=20°.
Ответ: /BOC=20°.
Поделитесь решением
Присоединяйтесь к нам...
Найдите площадь квадрата, описанного около окружности радиуса 32.
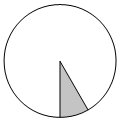Площадь круга равна 180. Найдите площадь сектора этого круга, центральный угол которого равен 30°.
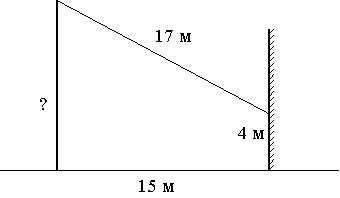От столба к дому натянут провод длиной 17 м, который закреплён на стене дома на высоте 4 м от земли (см. рисунок). Вычислите высоту столба, если расстояние от дома до столба равно 15 м.
Боковая сторона трапеции равна 5, а один из прилегающих к ней углов равен 30°. Найдите площадь трапеции, если её основания равны 3 и 9.
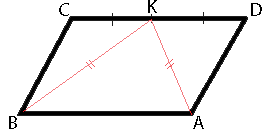В параллелограмме ABCD точка K — середина стороны CD. Известно, что KA=KB. Докажите, что данный параллелограмм — прямоугольник.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: