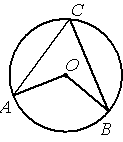
Точка О – центр окружности, /AOB=128° (см. рисунок). Найдите величину угла ACB (в градусах).
По условию /AOB=128°, этот угол является
центральным, соответственно дуга АВ (нижняя часть) тоже равна 128°. /ACB - является
вписанным углом и равен половине дуги, на которую опирается (
по теореме о вписанном угле). Соответственно, 128/2=64.
Ответ: /ACB=64°.
Поделитесь решением
Присоединяйтесь к нам...
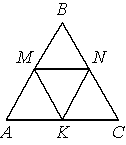В равностороннем треугольнике ABC точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что ВMKN — ромб.
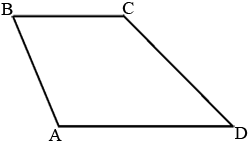Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=32.
Какие из данных утверждений верны? Запишите их номера.
1) Против большей стороны треугольника лежит меньший угол.
2) Любой квадрат можно вписать в окружность.
3) Площадь трапеции равна произведению средней линии на высоту.
В равнобедренном треугольнике ABC (АВ=ВС) точки M, N, K — середины сторон АВ, ВС, СА соответственно. Докажите, что треугольник MNK — равнобедренный.
Какие из данных утверждений верны? Запишите их номера.
1) Вокруг любого треугольника можно описать окружность.
2) Если в параллелограмме диагонали равны и перпендикулярны, то этот параллелограмм — квадрат.
3) Площадь трапеции равна произведению средней линии на высоту.
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: