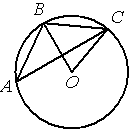
Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
По условию /BAC=20°, этот угол является
вписанным углом и равен половине градусной меры дуги, на которую опирается (
по теореме о вписанном угле).
Следовательно, градусная мера дуги, в нашей задаче, равна 20°*2=40°.
/BOC является
центральным и равен градусной мере дуги, на которую опирается, следовательно, /BOC=40°.
Ответ: /BOC=40°.
Поделитесь решением
Присоединяйтесь к нам...
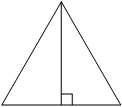Высота равностороннего треугольника равна 13√3. Найдите сторону этого треугольника.
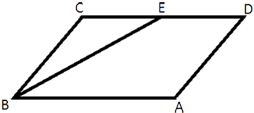Площадь параллелограмма
ABCD равна 30. Точка E – середина стороны CD. Найдите площадь трапеции ABED.
В треугольнике ABC угол C равен 90°, BC=5, AC=3.
Найдите tgB.
Основания BC и AD трапеции ABCD равны соответственно 5 и 45, BD=15. Докажите, что треугольники CBD и BDA подобны.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=24, BF=7.
Хочу получать новые решения
Ни какого спама
Дуга, на которую опирается центральный угол имеет ту же градусную меру. 
Автор: Таська
Комментарии: