
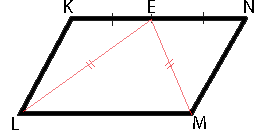
 В параллелограмме KLMN точка E — середина стороны KN. Известно, что EL=EM. Докажите, что данный параллелограмм — прямоугольник.
В параллелограмме KLMN точка E — середина стороны KN. Известно, что EL=EM. Докажите, что данный параллелограмм — прямоугольник.
Рассмотрим треугольники EKL и ENM. KE=EN, т.к. точка E - середина KN, EL=EM (из условия задачи), KL=NM (по свойству параллелограмма). Соответственно, треугольники EKL и ENM равны (по третьему признаку равенства треугольников).
Из равенства этих треугольников следует, что /EKL=/ENM.
KL||NM (по определению параллелограмма), рассмотрим сторону KN как секущую к этим параллельным сторонам. Тогда получается, что сумма углов EKL и ENM равна 180°, т.к. эти углы являются внутренними односторонними. Отсюда следует, что каждый из этих углов равен 90°.
Теперь рассмотрим стороны KN и LM, они параллельны (тоже по определению параллелограмма). Рассмотрим сторону KL как секущую к этим параллельным сторонам.
/NKL и /KLM - внутренние односторонние. Следовательно их сумма равна 180°. А так как /NKL=90°, то /KLM тоже равен 90°.
Аналогично доказывается, что /LMN тоже равен 90°.
Параллелограмм, у которого все углы прямые (т.е. 90°) называется прямоугольником (по определению).
Поделитесь решением
Присоединяйтесь к нам...
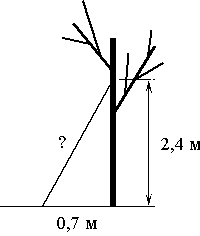 Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 0,7 м?
Какова длина (в метрах) лестницы, которую прислонили к дереву, если верхний её конец находится на высоте 2,4 м над землёй, а нижний отстоит от ствола дерева на 0,7 м?
 Четырёхугольник ABCD со сторонами AB=19 и CD=28 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
Четырёхугольник ABCD со сторонами AB=19 и CD=28 вписан в окружность. Диагонали AC и BD пересекаются в точке K, причём ∠
AKB=60°. Найдите радиус окружности, описанной около этого четырёхугольника.
 Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=12, BF=5.
Биссектрисы углов A и B при боковой стороне AB трапеции ABCD пересекаются в точке F. Найдите AB, если AF=12, BF=5.
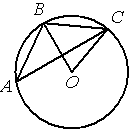 Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
Точка О – центр окружности, /BAC=20° (см. рисунок). Найдите величину угла BOC (в градусах).
 Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.
Найдите боковую сторону AB трапеции ABCD, если углы ABC и BCD равны соответственно 45° и 150°, а CD=26.

Комментарии: