
 В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
Рассмотрим треугольник АОВ. Этот треугольник
равнобедренный, т.к. ОА и ОВ - радиусы, поэтому они равны.
По
свойству равнобедренного треугольника /OAB=/OBA.
Рассмотрим треугольники АОВ и COD. /DOC=/AOB, т.к. они
вертикальные. СО=DO=OB=OA, т.к. это радиусы окружности.
Следовательно, треугольники АОВ и COD равны (по
первому признаку). Поэтому /OBA=/OAB=/ODC=/OCD=55°
Ответ: /OCD=55°.
Поделитесь решением
Присоединяйтесь к нам...
 В треугольнике ABC угол C прямой, AC=9, cosA=0,3. Найдите AB.
В треугольнике ABC угол C прямой, AC=9, cosA=0,3. Найдите AB.
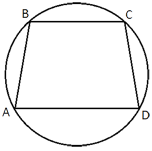 Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
Около трапеции, один из углов которой равен 49°, описана окружность. Найдите остальные углы трапеции.
 На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 4 м, а длинное плечо — 6 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 1 м?
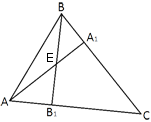 Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
Высоты AA1 и BB1 остроугольного треугольника ABC пересекаются в точке E. Докажите, что углы AA1B1 и ABB1 равны.
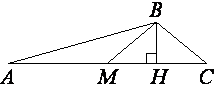 В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=64, HC=16 и ∠ACB=37°. Найдите угол AMB. Ответ дайте в градусах.
В треугольнике ABC BM – медиана и BH – высота. Известно, что AC=64, HC=16 и ∠ACB=37°. Найдите угол AMB. Ответ дайте в градусах.

Комментарии:
(2017-02-14 20:09:10) Администратор: Катя, была проблема у хостера, проблема устранена. Сейчас все читаемо?
(2017-02-14 14:50:46) Катя: не грузит решение, все в знаках вопроса. что такое??