
 –Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞
–Р–≤—В–Њ—А: –Ґ–∞—Б—М–Ї–∞–Ч–∞–і–∞—З–∞ вДЦ304 –Є–Ј 1087 |
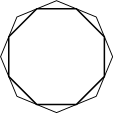 –Ф–∞–љ –њ—А–∞–≤–Є–ї—М–љ—Л–є –≤–Њ—Б—М–Љ–Є—Г–≥–Њ–ї—М–љ–Є–Ї. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –µ—Б–ї–Є –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ —Б–Њ–µ–і–Є–љ–Є—В—М –Њ—В—А–µ–Ј–Ї–∞–Љ–Є —Б–µ—А–µ–і–Є–љ—Л –µ–≥–Њ —Б—В–Њ—А–Њ–љ, —В–Њ –њ–Њ–ї—Г—З–Є—В—Б—П –њ—А–∞–≤–Є–ї—М–љ—Л–є –≤–Њ—Б—М–Љ–Є—Г–≥–Њ–ї—М–љ–Є–Ї.
–Ф–∞–љ –њ—А–∞–≤–Є–ї—М–љ—Л–є –≤–Њ—Б—М–Љ–Є—Г–≥–Њ–ї—М–љ–Є–Ї. –Ф–Њ–Ї–∞–ґ–Є—В–µ, —З—В–Њ –µ—Б–ї–Є –њ–Њ—Б–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ —Б–Њ–µ–і–Є–љ–Є—В—М –Њ—В—А–µ–Ј–Ї–∞–Љ–Є —Б–µ—А–µ–і–Є–љ—Л –µ–≥–Њ —Б—В–Њ—А–Њ–љ, —В–Њ –њ–Њ–ї—Г—З–Є—В—Б—П –њ—А–∞–≤–Є–ї—М–љ—Л–є –≤–Њ—Б—М–Љ–Є—Г–≥–Њ–ї—М–љ–Є–Ї.
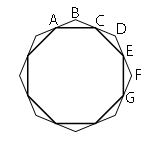 –Ґ–∞–Ї –Ї–∞–Ї —Г–≥–ї—Л –Љ–µ–љ—М—И–µ–≥–Њ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞—Б–њ–Њ–ї–∞–≥–∞—О—В—Б—П –љ–∞ —Б–µ—А–µ–і–Є–љ–µ —Б—В–Њ—А–Њ–љ, –∞ —Б—В–Њ—А–Њ–љ –≤–Њ—Б–µ–Љ—М, –Ј–љ–∞—З–Є—В –Є —Г–≥–ї–Њ–≤ –±—Г–і–µ—В –≤–Њ—Б–µ–Љ—М. –Ґ.–µ. –Љ–µ–љ—М—И–Є–є –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Є–Ї —П–≤–ї—П–µ—В—Б—П –≤–Њ—Б—М–Љ–Є—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–Љ. –Ґ–µ–њ–µ—А—М –і–Њ–Ї–∞–ґ–µ–Љ, —З—В–Њ –Њ–љ –њ—А–∞–≤–Є–ї—М–љ—Л–є.
–Ґ–∞–Ї –Ї–∞–Ї —Г–≥–ї—Л –Љ–µ–љ—М—И–µ–≥–Њ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ —А–∞—Б–њ–Њ–ї–∞–≥–∞—О—В—Б—П –љ–∞ —Б–µ—А–µ–і–Є–љ–µ —Б—В–Њ—А–Њ–љ, –∞ —Б—В–Њ—А–Њ–љ –≤–Њ—Б–µ–Љ—М, –Ј–љ–∞—З–Є—В –Є —Г–≥–ї–Њ–≤ –±—Г–і–µ—В –≤–Њ—Б–µ–Љ—М. –Ґ.–µ. –Љ–µ–љ—М—И–Є–є –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Є–Ї —П–≤–ї—П–µ—В—Б—П –≤–Њ—Б—М–Љ–Є—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–Љ. –Ґ–µ–њ–µ—А—М –і–Њ–Ї–∞–ґ–µ–Љ, —З—В–Њ –Њ–љ –њ—А–∞–≤–Є–ї—М–љ—Л–є.
–†–∞—Б—Б–Љ–Њ—В—А–Є–Љ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є ABC, CDE –Є EFG. AB=BC=CD=DE=EF=FG (–њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –њ—А–∞–≤–Є–ї—М–љ–Њ–≥–Њ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–∞).
/ABC=/CDE=/EFG (–њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –њ—А–∞–≤–Є–ї—М–љ–Њ–≥–Њ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–∞).
–°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, —А–∞—Б—Б–Љ–∞—В—А–Є–≤–∞–µ–Љ—Л–µ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Є —А–∞–≤–љ—Л (–њ–Њ
–њ–µ—А–≤–Њ–Љ—Г –њ—А–Є–Ј–љ–∞–Ї—Г —А–∞–≤–µ–љ—Б—В–≤–∞ —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤).
–≠—В–Њ –Њ–Ј–љ–∞—З–∞–µ—В, —З—В–Њ AC=CE=EG=GA.
–Ш–Ј —А–∞–≤–µ–љ—Б—В–≤–∞ —Н—В–Є—Е —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–Њ–≤ —В–∞–Ї–ґ–µ —Б–ї–µ–і—Г–µ—В, —З—В–Њ –≤—Б–µ –Є—Е –Њ—Б—В—А—Л–µ —Г–≥–ї—Л —В–Њ–ґ–µ —А–∞–≤–љ—Л (/BAC=/BCA=/DCE=...–Є —В.–і.). –°–ї–µ–і–Њ–≤–∞—В–µ–ї—М–љ–Њ, /ACE=/CEG=...–Є —В–∞–Ї –і–∞–ї–µ–µ
–Т –Є—В–Њ–≥–µ, –њ–Њ
–Њ–њ—А–µ–і–µ–ї–µ–љ–Є—О –њ—А–∞–≤–Є–ї—М–љ–Њ–≥–Њ –Љ–љ–Њ–≥–Њ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ –њ–Њ–ї—Г—З–∞–µ—В—Б—П, –Љ–µ–љ—М—И–Є–є –≤–Њ—Б—М–Љ–Є—Г–≥–Њ–ї—М–љ–Є–Ї - –њ—А–∞–≤–Є–ї—М–љ—Л–є.
–Я–Њ–і–µ–ї–Є—В–µ—Б—М —А–µ—И–µ–љ–Є–µ–Љ
–Я—А–Є—Б–Њ–µ–і–Є–љ—П–є—В–µ—Б—М –Ї –љ–∞–Љ...
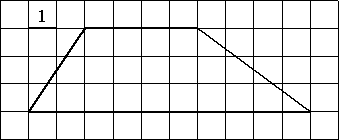 –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–є –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
–Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —В—А–∞–њ–µ—Ж–Є–Є, –Є–Ј–Њ–±—А–∞–ґ—С–љ–љ–Њ–є –љ–∞ —А–Є—Б—Г–љ–Ї–µ.
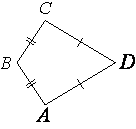 –Т –≤—Л–њ—Г–Ї–ї–Њ–Љ —З–µ—В—Л—А–µ—Е—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABCD –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ AB=BC, AD=CD, ∠B=133¬∞, ∠D=173¬∞. –Э–∞–є–і–Є—В–µ
—Г–≥–Њ–ї A. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–Т –≤—Л–њ—Г–Ї–ї–Њ–Љ —З–µ—В—Л—А–µ—Е—Г–≥–Њ–ї—М–љ–Є–Ї–µ ABCD –Є–Ј–≤–µ—Б—В–љ–Њ, —З—В–Њ AB=BC, AD=CD, ∠B=133¬∞, ∠D=173¬∞. –Э–∞–є–і–Є—В–µ
—Г–≥–Њ–ї A. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
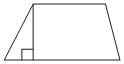 –Ю—Б–љ–Њ–≤–∞–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ—Л 5 –Є 13, –∞ –≤—Л—Б–Њ—В–∞ —А–∞–≤–љ–∞ 9. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є.
–Ю—Б–љ–Њ–≤–∞–љ–Є—П —В—А–∞–њ–µ—Ж–Є–Є —А–∞–≤–љ—Л 5 –Є 13, –∞ –≤—Л—Б–Њ—В–∞ —А–∞–≤–љ–∞ 9. –Э–∞–є–і–Є—В–µ –њ–ї–Њ—Й–∞–і—М —Н—В–Њ–є —В—А–∞–њ–µ—Ж–Є–Є.
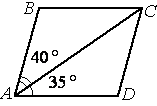 –Ф–Є–∞–≥–Њ–љ–∞–ї—М AC –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –Њ–±—А–∞–Ј—Г–µ—В —Б –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ 40¬∞ –Є 35¬∞. –Э–∞–є–і–Є—В–µ –±–Њ–ї—М—И–Є–є —Г–≥–Њ–ї –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
–Ф–Є–∞–≥–Њ–љ–∞–ї—М AC –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞ ABCD –Њ–±—А–∞–Ј—Г–µ—В —Б –µ–≥–Њ —Б—В–Њ—А–Њ–љ–∞–Љ–Є —Г–≥–ї—Л, —А–∞–≤–љ—Л–µ 40¬∞ –Є 35¬∞. –Э–∞–є–і–Є—В–µ –±–Њ–ї—М—И–Є–є —Г–≥–Њ–ї –њ–∞—А–∞–ї–ї–µ–ї–Њ–≥—А–∞–Љ–Љ–∞.
 –°—В–Њ—А–Њ–љ–∞ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –Э–∞–є–і–Є—В–µ ∠C, –µ—Б–ї–Є ∠A=30¬∞. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.
–°—В–Њ—А–Њ–љ–∞ AC —В—А–µ—Г–≥–Њ–ї—М–љ–Є–Ї–∞ ABC –њ—А–Њ—Е–Њ–і–Є—В —З–µ—А–µ–Ј —Ж–µ–љ—В—А –Њ–Ї—А—Г–ґ–љ–Њ—Б—В–Є. –Э–∞–є–і–Є—В–µ ∠C, –µ—Б–ї–Є ∠A=30¬∞. –Ю—В–≤–µ—В –і–∞–є—В–µ –≤ –≥—А–∞–і—Г—Б–∞—Е.



–Ъ–Њ–Љ–Љ–µ–љ—В–∞—А–Є–Є: