
 –ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į
–ź–≤—ā–ĺ—Ä: –Ę–į—Ā—Ć–ļ–į–ó–į–ī–į—á–į ‚ĄĖ100 –ł–∑ 1087 |
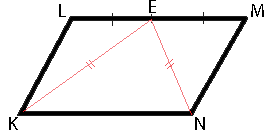 –í –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–Ķ KLMN —ā–ĺ—á–ļ–į E ‚ÄĒ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ—č LM. –ė–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ EK=EN. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ –ī–į–Ĺ–Ĺ—č–Ļ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ ‚ÄĒ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ.
–í –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–Ķ KLMN —ā–ĺ—á–ļ–į E ‚ÄĒ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į —Ā—ā–ĺ—Ä–ĺ–Ĺ—č LM. –ė–∑–≤–Ķ—Ā—ā–Ĺ–ĺ, —á—ā–ĺ EK=EN. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ –ī–į–Ĺ–Ĺ—č–Ļ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ ‚ÄĒ –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ.
–†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł KLE –ł NME. LE=ME, —ā.–ļ. —ā–ĺ—á–ļ–į E - —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–į LM, EK=EN –ł–∑ —É—Ā–Ľ–ĺ–≤–ł—Ź –∑–į–ī–į—á–ł, LK=MN (–Ņ–ĺ —Ā–≤–ĺ–Ļ—Ā—ā–≤—É –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į). –°–ĺ–ĺ—ā–≤–Ķ—ā—Ā—ā–≤–Ķ–Ĺ–Ĺ–ĺ, —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ł KLE –ł NME —Ä–į–≤–Ĺ—č (–Ņ–ĺ —ā—Ä–Ķ—ā—Ć–Ķ–ľ—É –Ņ—Ä–ł–∑–Ĺ–į–ļ—É —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤).
–ė–∑ —Ä–į–≤–Ķ–Ĺ—Ā—ā–≤–į —ć—ā–ł—Ö —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–≤ —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ /KLE=/NME.
LK||MN (–Ņ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į), —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —Ā—ā–ĺ—Ä–ĺ–Ĺ—É LM –ļ–į–ļ —Ā–Ķ–ļ—É—Č—É—é –ļ —ć—ā–ł–ľ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č–ľ —Ā—ā–ĺ—Ä–ĺ–Ĺ–į–ľ. –Ę–ĺ–≥–ī–į –Ņ–ĺ–Ľ—É—á–į–Ķ—ā—Ā—Ź, —á—ā–ĺ —Ā—É–ľ–ľ–į —É–≥–Ľ–ĺ–≤ KLE –ł NME —Ä–į–≤–Ĺ–į 180¬į, —ā.–ļ. —ć—ā–ł —É–≥–Ľ—č —Ź–≤–Ľ—Ź—é—ā—Ā—Ź –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–ł–ľ–ł –ĺ–ī–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–ł–ľ–ł. –ě—ā—Ā—é–ī–į —Ā–Ľ–Ķ–ī—É–Ķ—ā, —á—ā–ĺ –ļ–į–∂–ī—č–Ļ –ł–∑ —ć—ā–ł—Ö —É–≥–Ľ–ĺ–≤ —Ä–į–≤–Ķ–Ĺ 90¬į.
–Ę–Ķ–Ņ–Ķ—Ä—Ć —Ä–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —Ā—ā–ĺ—Ä–ĺ–Ĺ—č LM –ł KN, –ĺ–Ĺ–ł –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č (—ā–ĺ–∂–Ķ –Ņ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ–į). –†–į—Ā—Ā–ľ–ĺ—ā—Ä–ł–ľ —Ā—ā–ĺ—Ä–ĺ–Ĺ—É KL –ļ–į–ļ —Ā–Ķ–ļ—É—Č—É—é –ļ —ć—ā–ł–ľ –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č–ľ —Ā—ā–ĺ—Ä–ĺ–Ĺ–į–ľ.
/KLE –ł /LKN - –≤–Ĺ—É—ā—Ä–Ķ–Ĺ–Ĺ–ł–Ķ –ĺ–ī–Ĺ–ĺ—Ā—ā–ĺ—Ä–ĺ–Ĺ–Ĺ–ł–Ķ. –°–Ľ–Ķ–ī–ĺ–≤–į—ā–Ķ–Ľ—Ć–Ĺ–ĺ –ł—Ö —Ā—É–ľ–ľ–į —Ä–į–≤–Ĺ–į 180¬į. –ź —ā–į–ļ –ļ–į–ļ /KLE=90¬į, —ā–ĺ /LKN —ā–ĺ–∂–Ķ —Ä–į–≤–Ķ–Ĺ 90¬į.
–ź–Ĺ–į–Ľ–ĺ–≥–ł—á–Ĺ–ĺ –ī–ĺ–ļ–į–∑—č–≤–į–Ķ—ā—Ā—Ź, —á—ā–ĺ /MNK —ā–ĺ–∂–Ķ —Ä–į–≤–Ķ–Ĺ 90¬į.
–ü–į—Ä–į–Ľ–Ľ–Ķ–Ľ–ĺ–≥—Ä–į–ľ–ľ, —É –ļ–ĺ—ā–ĺ—Ä–ĺ–≥–ĺ –≤—Ā–Ķ —É–≥–Ľ—č –Ņ—Ä—Ź–ľ—č–Ķ (—ā.–Ķ. 90¬į) –Ĺ–į–∑—č–≤–į–Ķ—ā—Ā—Ź –Ņ—Ä—Ź–ľ–ĺ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–ĺ–ľ (–Ņ–ĺ –ĺ–Ņ—Ä–Ķ–ī–Ķ–Ľ–Ķ–Ĺ–ł—é).
–ü–ĺ–ī–Ķ–Ľ–ł—ā–Ķ—Ā—Ć —Ä–Ķ—ą–Ķ–Ĺ–ł–Ķ–ľ
–ü—Ä–ł—Ā–ĺ–Ķ–ī–ł–Ĺ—Ź–Ļ—ā–Ķ—Ā—Ć –ļ –Ĺ–į–ľ...
 –ü—Ä—Ź–ľ—č–Ķ m –ł n –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č. –Ě–į–Ļ–ī–ł—ā–Ķ ∠3, –Ķ—Ā–Ľ–ł ∠1=22¬į, ∠2=72¬į. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–ü—Ä—Ź–ľ—č–Ķ m –ł n –Ņ–į—Ä–į–Ľ–Ľ–Ķ–Ľ—Ć–Ĺ—č. –Ě–į–Ļ–ī–ł—ā–Ķ ∠3, –Ķ—Ā–Ľ–ł ∠1=22¬į, ∠2=72¬į. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
 –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć, –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–į—Ź –≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ ABC, –ļ–į—Ā–į–Ķ—ā—Ā—Ź –Ķ–≥–ĺ —Ā—ā–ĺ—Ä–ĺ–Ĺ –≤ —ā–ĺ—á–ļ–į—Ö M, K –ł P. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–Ľ—č —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC, –Ķ—Ā–Ľ–ł —É–≥–Ľ—č —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į MKP —Ä–į–≤–Ĺ—č 44¬į, 71¬į –ł 65¬į.
–ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć, –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–į—Ź –≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ ABC, –ļ–į—Ā–į–Ķ—ā—Ā—Ź –Ķ–≥–ĺ —Ā—ā–ĺ—Ä–ĺ–Ĺ –≤ —ā–ĺ—á–ļ–į—Ö M, K –ł P. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–Ľ—č —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC, –Ķ—Ā–Ľ–ł —É–≥–Ľ—č —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į MKP —Ä–į–≤–Ĺ—č 44¬į, 71¬į –ł 65¬į.
 –ö–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ –ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ O –≤ —ā–ĺ—á–ļ–į—Ö A –ł B –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –Ņ–ĺ–ī —É–≥–Ľ–ĺ–ľ 82¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ABO. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
–ö–į—Ā–į—ā–Ķ–Ľ—Ć–Ĺ—č–Ķ –ļ –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ O –≤ —ā–ĺ—á–ļ–į—Ö A –ł B –Ņ–Ķ—Ä–Ķ—Ā–Ķ–ļ–į—é—ā—Ā—Ź –Ņ–ĺ–ī —É–≥–Ľ–ĺ–ľ 82¬į. –Ě–į–Ļ–ī–ł—ā–Ķ —É–≥–ĺ–Ľ ABO. –ě—ā–≤–Ķ—ā –ī–į–Ļ—ā–Ķ –≤ –≥—Ä–į–ī—É—Ā–į—Ö.
 –Ě–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ –ź–° —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ź–í–° –≤—č–Ī—Ä–į–Ĺ—č —ā–ĺ—á–ļ–ł D –ł E —ā–į–ļ, —á—ā–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–ł AD –ł CE —Ä–į–≤–Ĺ—č (—Ā–ľ. —Ä–ł—Ā—É–Ĺ–ĺ–ļ). –ě–ļ–į–∑–į–Ľ–ĺ—Ā—Ć, —á—ā–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–ł BD –ł BE —ā–ĺ–∂–Ķ —Ä–į–≤–Ĺ—č. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –ź–í–° ‚ÄĒ —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–Ļ.
–Ě–į —Ā—ā–ĺ—Ä–ĺ–Ĺ–Ķ –ź–° —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ź–í–° –≤—č–Ī—Ä–į–Ĺ—č —ā–ĺ—á–ļ–ł D –ł E —ā–į–ļ, —á—ā–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–ł AD –ł CE —Ä–į–≤–Ĺ—č (—Ā–ľ. —Ä–ł—Ā—É–Ĺ–ĺ–ļ). –ě–ļ–į–∑–į–Ľ–ĺ—Ā—Ć, —á—ā–ĺ –ĺ—ā—Ä–Ķ–∑–ļ–ł BD –ł BE —ā–ĺ–∂–Ķ —Ä–į–≤–Ĺ—č. –Ē–ĺ–ļ–į–∂–ł—ā–Ķ, —á—ā–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ –ź–í–° ‚ÄĒ —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ—č–Ļ.
–ě—Ā–Ĺ–ĺ–≤–į–Ĺ–ł–Ķ AC —Ä–į–≤–Ĺ–ĺ–Ī–Ķ–ī—Ä–Ķ–Ĺ–Ĺ–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į ABC —Ä–į–≤–Ĺ–ĺ 6. –ě–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā—Ć —Ä–į–ī–ł—É—Ā–į 4,5 —Ā —Ü–Ķ–Ĺ—ā—Ä–ĺ–ľ –≤–Ĺ–Ķ —ć—ā–ĺ–≥–ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ļ–į—Ā–į–Ķ—ā—Ā—Ź –Ņ—Ä–ĺ–ī–ĺ–Ľ–∂–Ķ–Ĺ–ł—Ź –Ī–ĺ–ļ–ĺ–≤—č—Ö —Ā—ā–ĺ—Ä–ĺ–Ĺ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ–į –ł –ļ–į—Ā–į–Ķ—ā—Ā—Ź –ĺ—Ā–Ĺ–ĺ–≤–į–Ĺ–ł—Ź AC –≤ –Ķ–≥–ĺ —Ā–Ķ—Ä–Ķ–ī–ł–Ĺ–Ķ. –Ě–į–Ļ–ī–ł—ā–Ķ —Ä–į–ī–ł—É—Ā –ĺ–ļ—Ä—É–∂–Ĺ–ĺ—Ā—ā–ł, –≤–Ņ–ł—Ā–į–Ĺ–Ĺ–ĺ–Ļ –≤ —ā—Ä–Ķ—É–≥–ĺ–Ľ—Ć–Ĺ–ł–ļ ABC.



–ö–ĺ–ľ–ľ–Ķ–Ĺ—ā–į—Ä–ł–ł: