На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=7. Площадь треугольника ABC равна 60. Найдите площадь треугольника ABD.
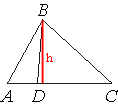Проведем высоту из вершины B.
Заметим, что это высота не только треугольника ABC, но и треугольника ABD.
Найдем высоту, используя формулу площади треугольника для треугольника ABC:
SABC=AC*h/2=(AD+DC)*h/2
60=(5+7)*h/2
60=12*h/2
60=6*h
h=10
Теперь применим эту же формулу для треугольника ABD:
SABD=AD*h/2=5*10/2=5*5=25
Ответ: 25
Поделитесь решением
Присоединяйтесь к нам...
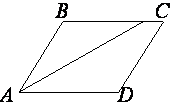Найдите величину острого угла параллелограмма ABCD, если биссектриса угла A образует со стороной BC угол, равный 1°. Ответ дайте в градусах.
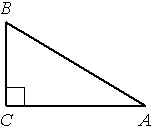В треугольнике ABC угол C прямой, BC=4, sinA=0,8. Найдите AB.
Синус острого угла A треугольника ABC равен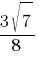 
. Найдите CosA.
Прямая, параллельная стороне
AC треугольника ABC, пересекает стороны AB и BC в точках K и M соответственно. Найдите AC, если BK:KA=3:4, KM=18.
В трапецию, сумма длин боковых сторон которой равна 24, вписана окружность. Найдите длину средней линии трапеции.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: