
 В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
В равнобедренной трапеции основания равны 3 и 7, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.
 Проведем высоты как показано на рисунке. И рассмотрим треугольник CDF. Это
прямоугольный треугольник (т.к. /CFD - прямой).
Проведем высоты как показано на рисунке. И рассмотрим треугольник CDF. Это
прямоугольный треугольник (т.к. /CFD - прямой).
По
теореме о сумме углов треугольника найдем угол FCD
/FCD=180°-90°-45°=45°. Заметим, что /FCD=/FDC. Следовательно, треугольник
равнобедренный (по
свойству равнобедренного треугольника). Отсюда следует, что FD=FC (по
определению равнобедренного треугольника).
Рассмотрим треугольник ABE. /BAE=/FDC=45° (т.к. по условию задачи
трапеция равнобедренная).
Аналогично по
теореме о сумме углов треугольника получим, что /ABE=180°-90°-45°=45°, а следовательно (аналогично предыдущему треугольнику) треугольник ABE -
равнобедренный.
Причем эти треугольники равны (AB=CD, BE=CF и /ABE=/FCD -
первый признак равенства)=> AE=FD.
Рассмотрим четырехугольник BCFE.
Т.к. BC||EF, BE и FC - высоты, следовательно /BEF=90°=/CFE. /EBC=/BCF=90°. Следовательно четырехугольник BCFE -
прямоугольник => BC=EF.
Теперь можем записать:
AD=AE+EF+FD, 7=AE+3+FD, 7=AE+3+AE
4=2*AE => AE=2.
Т.к. AE=BE=2, а BE-высота трапеции, то теперь можем вычислить
площадь трапеции.
Sтрапеции=BE*(BC+AD)/2
Sтрапеции=2*(3+7)/2=10.
Ответ: Sтрапеции=10.
Поделитесь решением
Присоединяйтесь к нам...
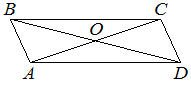 Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.
Диагонали AC и BD параллелограмма ABCD пересекаются в точке O, AC=12, BD=20, AB=7. Найдите DO.
 Точка О – центр окружности, /AOB=72° (см. рисунок). Найдите величину угла ACB (в градусах).
Точка О – центр окружности, /AOB=72° (см. рисунок). Найдите величину угла ACB (в градусах).
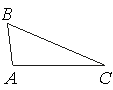 В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
В треугольнике ABC известно, что AB=3, BC=8, AC=7. Найдите cos∠ABC.
 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
 В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.
В окружности с центром в точке О проведены диаметры AD и BC, угол ABO равен 55°. Найдите величину угла ODC.

Комментарии: