Укажите номера верных утверждений.
1) Диагонали любого прямоугольника равны.
2) Если в треугольнике есть один острый угол, то этот треугольник остроугольный.
3) Если точка лежит на биссектрисе угла, то она равноудалена от сторон этого угла.
Рассмотрим каждое утверждение.
1) "Диагонали любого
прямоугольника равны" - это утверждение верно, т.к. является одним из
свойств прямоугольника.
2) "Если в треугольнике есть один острый угол, то этот треугольник остроугольный" - это утверждение неверно, т.к. не соответствует
определению остроугольного треугольника.
3) "Если точка лежит на
биссектрисе угла, то она равноудалена от сторон этого угла". Расстояние от точки до прямой - отрезок, проведенный из данной точки перпендикулярно прямой.
Рассмотрим рисунок.
Треугольники ABD и BCD -
прямоугольные, т.к. AD и DC - расстояние от точки D (расположенной на биссектрисе) до лучей угла. Сторона BD - общая для этих треугольников, /ABD=/CBD, по
определению биссектрисы. Следовательно,
синусы этих углов тоже равны.
По
определению синуса, sin(ABD)=sin(CBD)=AD/BD=CD/BD, следовательно AD=CD. Т.е. это утверждение верно.
Поделитесь решением
Присоединяйтесь к нам...
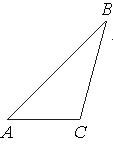В треугольнике ABC угол A равен 45°, угол B равен 30°, BC=8√2. Найдите AC.
Точка О – центр окружности, /BOC=110° (см. рисунок). Найдите величину угла BAC (в градусах).
Укажите номера верных утверждений.
1) Центр вписанной окружности равнобедренного треугольника лежит на высоте, проведённой к основанию треугольника.
2) Ромб не является параллелограммом.
3) Сумма острых углов прямоугольного треугольника равна 90°.
Стороны AC, AB, BC треугольника ABC равны 2√
Касательные к окружности с центром O в точках A и B пересекаются под углом 76°. Найдите угол ABO. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: