Окружность с центром на стороне AC треугольника ABC проходит через вершину C и касается прямой AB в точке B. Найдите диаметр окружности, если AB=6, AC=10.
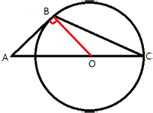OC является радиусом окружности R, AO=AC-OC.
Проведем отрезок BO. BO - так же является радиусом окружности. AB -
касательная к окружности, следовательно AB перпендикулярен BO (по
свойству касательной).
Значит треугольник ABO -
прямоугольный, тогда по
теореме Пифагора:
AO2=AB2+BO2
(AC-OC)2=AB2+R2
(10-R)2=62+R2
100-20R+R2=36+R2
100-36=20R
R=3,2
D=2R=2*3,2=6,4
Ответ: D=6,4
Поделитесь решением
Присоединяйтесь к нам...
Боковые стороны AB и CD трапеции ABCD равны соответственно 12 и 20, а основание BC равно 2. Биссектриса угла ADC проходит через середину стороны AB. Найдите площадь трапеции.
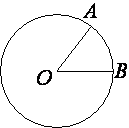На окружности с центром в точке O отмечены точки A и B так, что ∠AOB=66°. Длина меньшей дуги AB равна 99. Найдите длину большей дуги AB.
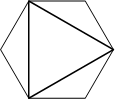Дан правильный шестиугольник. Докажите, что если его вершины последовательно соединить отрезками через одну, то получится равносторонний треугольник.
В выпуклом четырёхугольнике NPQM диагональ NQ является биссектрисой угла PNM и пересекается с диагональю PM в точке S. Найдите NS, если известно, что около четырёхугольника NPQM можно описать окружность, PQ=44, SQ=16.
В треугольнике АВС углы А и С равны 30° и 50° соответственно. Найдите угол между высотой ВН и биссектрисой BD.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии:
(2019-06-03 21:37:20) Администратор: Владимир, AB-касательная по условию задачи, а касательная перпендикулярна радиусу по свойству касательной.
(2019-06-02 11:11:48) владимир: Почему АВ должна быть касательной?
(2019-06-02 11:06:33) владимир: Почему угол ABO(О-центр окружности)является прямым?