
 Сторона квадрата равна 4√2. Найдите радиус окружности, описанной около этого квадрата.
Сторона квадрата равна 4√2. Найдите радиус окружности, описанной около этого квадрата.
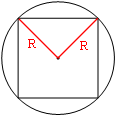 Проведем отрезки из центра
квадрата к двум его углам, как на рисунке.
Проведем отрезки из центра
квадрата к двум его углам, как на рисунке.
Заметим, что:
1) Эти отрезки и являются радиусами окружности.
2) Получившийся треугольник является
прямоугольным (по свойству квадрата).
Тогда мы можем применить
теорему Пифагора (пусть сторона квадрата - это "а"):
a2=R2+R2
a2=2R2
(4√2)2=2R2
16*2=2R2 |:2
16=R2
R=√16=4
Ответ: 4
Поделитесь решением
Присоединяйтесь к нам...
Основание AC равнобедренного треугольника ABC равно 10. Окружность радиуса 9 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
 Периметр квадрата равен 184. Найдите площадь квадрата.
Периметр квадрата равен 184. Найдите площадь квадрата.
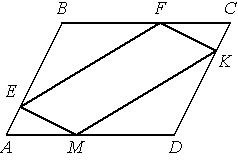 В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
В параллелограмме АВСD точки E, F, K и М лежат на его сторонах, как показано на рисунке, причём АЕ = CK, BF = DM. Докажите, что EFKM — параллелограмм.
 Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
Прямая AD, перпендикулярная медиане ВМ треугольника АВС, делит угол ВАС пополам. Найдите сторону АС, если сторона АВ равна 3.
 В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.
В трапеции ABCD AB=CD, AC=AD и ∠ABC=123°. Найдите угол CAD. Ответ дайте в градусах.

Комментарии: