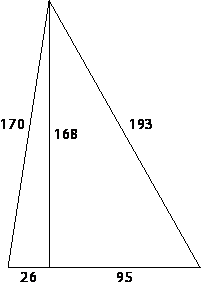Найдите площадь треугольника, изображённого на рисунке.
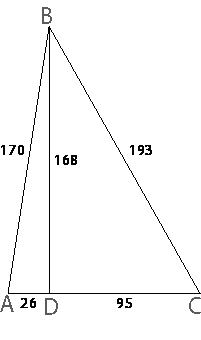Обозначим ключевые точки как показано на рисунке.
Проверим, является ли BD
высотой данного треугольника. Если является, то треугольник ABD -
прямоугольный и к нему применима
теорема Пифагора:
AB2=AD2+BD2
1702=262+1682
28900=676+28224
28900=28900
Равенство выполняется.
Площадь треугольника равна произведению
высоты на половину стороны, к которой проведена
высота.
SABC=BD*AC/2=BD*(AD+DC)/2=168*(26+95)/2=84*121=10164
Ответ: SABC=10164
Поделитесь решением
Присоединяйтесь к нам...
Радиус вписанной в квадрат окружности равен 22√2. Найдите диагональ этого квадрата.
Диагональ прямоугольника образует угол 75° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.
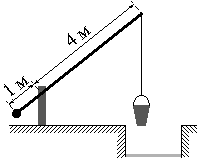На рисунке изображён колодец с «журавлём». Короткое плечо имеет длину 1 м, а длинное плечо — 4 м. На сколько метров опустится конец длинного плеча, когда конец короткого поднимется на 0,5 м?
Точка O – центр окружности, на которой лежат точки S, T и V таким образом, что OSTV – ромб. Найдите угол OVT. Ответ дайте в градусах.
На окружности по разные стороны от диаметра AB взяты точки M и N. Известно, что
∠NBA=47°. Найдите угол NMB. Ответ дайте в градусах.
Хочу получать новые решения
Ни какого спама
Автор: Таська
Комментарии: