
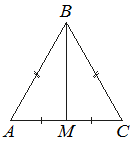 В равнобедренном треугольнике ABC медиана BM, проведённая к основанию, равна 12, а tgA=12/5. Найдите длину боковой стороны треугольника ABC.
В равнобедренном треугольнике ABC медиана BM, проведённая к основанию, равна 12, а tgA=12/5. Найдите длину боковой стороны треугольника ABC.
По
третьему свойству равнобедренного треугольника, BM является не только медианой, но и
высотой.
Следовательно, треугольник ABM -
прямоугольный.
Тогда tgA=BM/AM (по определению tg).
А так как по условию thA=12/5, то:
BM/AM=12/5
12/AM=12/5 |:12
1/AM=1/5
AM=5
AM и BM - катеты треугольника ABM. Необходимо найти AB. Воспользуемся
теоремой Пифагора:
AB2=AM2+BM2
AB2=52+122
AB2=25+144=169
AB=√169=13
Ответ: 13
Поделитесь решением
Присоединяйтесь к нам...
 Какой наименьший угол (в градусах) образуют минутная
и часовая стрелки часов в 17:00?
Какой наименьший угол (в градусах) образуют минутная
и часовая стрелки часов в 17:00?
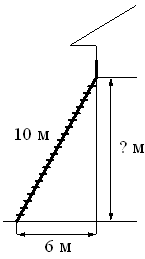 Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте расположено окно? Ответ дайте в метрах.
Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте расположено окно? Ответ дайте в метрах.
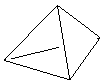 Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
Стороны основания правильной треугольной пирамиды равны 16, а боковые рёбра равны 17. Найдите площадь боковой поверхности этой пирамиды.
 Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 11:00?
Какой наименьший угол (в градусах) образуют минутная и часовая стрелки часов в 11:00?
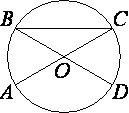 В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 124°. Найдите угол ACB. Ответ дайте в градусах.
В окружности с центром O отрезки AC и BD — диаметры. Центральный угол AOD равен 124°. Найдите угол ACB. Ответ дайте в градусах.

Комментарии: