
 Точка O – центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR – ромб. Найдите угол ORQ. Ответ дайте в градусах.
Точка O – центр окружности, на которой лежат точки P, Q и R таким образом, что OPQR – ромб. Найдите угол ORQ. Ответ дайте в градусах.
FO=RO (т.к. это радиусы окружности)
FO=RO=FQ=QR (по
определению ромба)
 Проведем отрезок OQ.
Проведем отрезок OQ.
OQ тоже радиус окружности, следовательно OQ=FO=RO=FQ=QR
Следовательно, треугольники FQO и QRO -
равносторонние, а все углы равностороннего треугольника равны 60° (по
свойству).
Следовательно, /ORQ=60°
Ответ: 60
Поделитесь решением
Присоединяйтесь к нам...
 Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
Длина хорды окружности равна 72, а расстояние от центра окружности до этой хорды равно 27. Найдите диаметр окружности.
 Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны
AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.
Медиана BM и биссектриса AP треугольника ABC пересекаются в точке K, длина стороны
AC втрое больше длины стороны AB. Найдите отношение площади четырехугольника KPCM к площади треугольника ABC.
 Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.
Биссектриса угла A параллелограмма ABCD пересекает сторону BC
в точке K. Найдите периметр параллелограмма, если BK=5, CK=14.
Основание AC равнобедренного треугольника ABC равно 18. Окружность радиуса 12 с центром вне этого треугольника касается продолжения боковых сторон треугольника и касается основания AC в его середине. Найдите радиус окружности, вписанной в треугольник ABC.
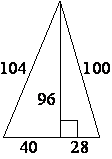 Найдите площадь треугольника, изображённого на рисунке.
Найдите площадь треугольника, изображённого на рисунке.
Комментарии: