ОГЭ, Математика.
Геометрия: Задача №1BD0AE

Задача №674 из 1087
Условие задачи:

Диагональ прямоугольника образует угол 51° с одной из его сторон. Найдите угол между диагоналями этого прямоугольника. Ответ дайте в градусах.

Решение задачи:

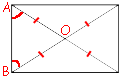Диагонали прямоугольника равны и точкой пересечения делятся пополам (по свойству прямоугольника).
Рассмотрим треугольник ABO (см. рисунок).
AO=BO (как мы только что выяснили).
Следовательно, треугольник ABO - равнобедренный.
По первому свойству равнобедренного треугольника:
∠OBA=∠OAB
По теореме о сумме углов треугольника:
180°=∠AOB+∠OBA+∠OAB
180°=∠AOB+51°+51°
180°=∠AOB+102°
∠AOB=180°-102°
∠AOB=78°
Ответ: 78

Поделитесь решением

Присоединяйтесь к нам...

Вы можете поблагодарить автора, написать свои претензии или предложения на странице 'Про нас'

Другие задачи из этого раздела

Задача №07740D

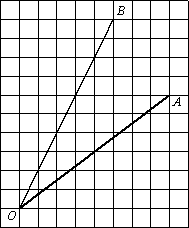Найдите тангенс угла AOB.

Задача №1EE527

В равнобедренную трапецию, периметр которой равен 180, а площадь равна 1620, можно вписать окружность. Найдите расстояние от точки пересечения диагоналей трапеции до её меньшего основания.

Задача №0D90BE

Окружность, вписанная в треугольник ABC, касается его сторон в точках M, K и P. Найдите углы треугольника ABC, если углы треугольника MKP равны 38°, 78° и 64°.